
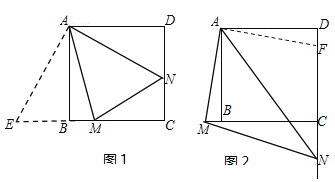
【题目】已知:正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB,DC(或它们的延长线)于点M,N.当∠MAN绕点A旋转到BM=DN时(如图1),易证BM+DN=MN.

(1)当∠MAN绕点A旋转到BM≠DN时(如图2),线段BM,DN和MN之间有怎样的数量关系?写出猜想,并加以证明.
(2)当∠MAN绕点A旋转到如图3的位置时,线段BM,DN和MN之间又有怎样的数量关系?请直接写出你的猜想.
【答案】(1)BM+DN=MN成立.(2)DN-BM=MN.
【解析】试题分析:(1)、在MB的延长线上,截得BE=DN,连接AE得到△ABE≌△AND,从而得到AE=AN,然后证明△AEM≌△ANM,得到ME=MN,从而得出答案;(2)、在DC上截取DF=BM,连接AF得到△ABM≌△ADF,然后证明△MAN≌△FAN,得到所求的答案.
试题解析:(1)、BM+DN=MN成立.
如下图1,在MB的延长线上,截得BE=DN,连接AE,易证:△ABE≌△AND,∴AE=AN.
∴∠EAB=∠NMD.∴∠BAD=90°,∠NAM=45°
∴∠BAM+∠NMD=45°.∴∠EAB+∠BAM=45°.∴∠EAM=∠NAM![]() 又AM为公共边,∴△AEM≌△ANM,
又AM为公共边,∴△AEM≌△ANM,
∴ME=MN,∴ME=BE+BM=DN+BM.∴DN+BM=MN.
(2)、DN-BM=MN.
如图2,在DC上截取DF=BM,连接AF.∵AB=AD,∠ABM=∠ADF=90°,∴△ABM≌△ADF(SAS)
∴AM=AF,∠MAB=∠FAD.∴∠MAB+∠BAF=∠FAD+∠BAF=90°,即∠MAF=∠BAD=90°.
又∠MAN=45°,∴∠NAF=∠MAN=45°.∵AN=AN,∴△MAN≌△FAN.∴MN=FN,即MN=DN-DF=DN-BM;


科目:初中数学 来源: 题型:
【题目】某市语委办为了解本市八年级学生汉字书写能力情况,随机抽查了部分八年级学生,并将调查数据进行如下整理,请解答以下问题:
正确书写出的字数x(个) | 频数(人) | 频率 |
0≤x≤5 | 8 | 0.16 |
5<x≤10 | ||
10<x≤15 | 16 | 0.32 |
15<x≤20 | 8 | 0.16 |
20<x≤25 | 4 | 0.08 |
25<x≤30 | 2 | 0.04 |
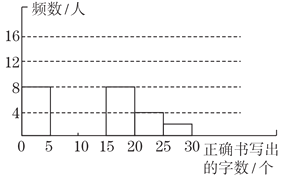
(1)把频数、频率分布表和频数分布直方图补充完整;
(2)根据统计图,可知“正确书写的字数”的中位数应处的范围是________;
(3)若正确书写的字数不超过15个为不及格,请求出不及格人数占所抽查人数的百分比;并根据调查数据估计,该市20 000名八年级学生中,有多少名学生不及格?对此,请你用一句话谈谈你的建议或感想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下是一位同学所做的有理数运算解题过程的一部分: 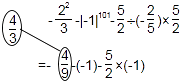
(1)请你在上面的解题过程中仿照给出的方式,圈画出他的错误之处,并将正确结果写在相应的圈内;
(2)请就此题反映出的该同学有理数运算掌握的情况进行具体评价,并对相应的有效避错方法给出你的建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
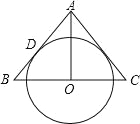
【题目】如图,AO是△ABC的中线,⊙O与AB边相切于点D.
(1)要使⊙O与AC边也相切,应增加条件 (任写一个);
(2)增加条件后,请你说明⊙O与AC边相切的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,纸片□ABCD中,AD=5,S□ABCD=15,过点A作AE⊥BC,垂足为E,沿AE剪下△ABE,将它平移至△DCE'的位置,拼成四边形AEE'D,则四边形AEE'D的形状为( )
A.平行四边形 B.菱形 C.矩形 D.正方形
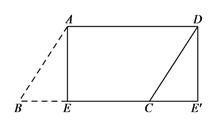
(2)如图,在(1)中的四边形纸片AEE'D中,在EE'上取一点F,使EF=4,剪下△AEF,剪下△AEF,将它平移至△DE'F'的位置,拼成四边形AFF'D.
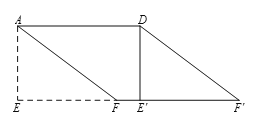
①求证:四边形AFF'D是菱形;
②求四边形AFF'D的两条对角线的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC,以BC为直径的⊙O交AC于点D,过点D作DE⊥AB,DF⊥BC,垂足分别为E、F.
(1)求证:ED是⊙O的切线;
(2)若DF=3![]() ,cosA=
,cosA=![]() ,求⊙O的直径.
,求⊙O的直径.
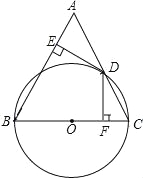
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=﹣1,且过点(﹣3,0),下列说法:
①b2﹣4ac=0;
②4a+2b+c<0;
③3a+c=0;
④若(﹣5,y1),(2,y2)是抛物线上的两点,则y1>y2,
其中正确的是( )
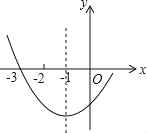
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
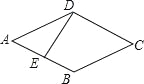
【题目】如图,点E是菱形ABCD边上一动点,它沿A→B→C→D的路径移动,设点E经过的路径长为x,△ADE的面积为y,下列图象中能反映y与x函数关系的是( )
A.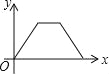
B.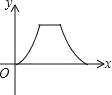
C.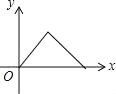
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com