
【题目】如图,在△ABC中,AB=BC,以BC为直径的⊙O交AC于点D,过点D作DE⊥AB,DF⊥BC,垂足分别为E、F.
(1)求证:ED是⊙O的切线;
(2)若DF=3![]() ,cosA=
,cosA=![]() ,求⊙O的直径.
,求⊙O的直径.
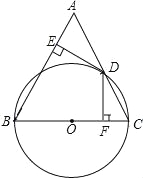
【答案】(1)证明见解析;
(2)⊙O的直径为![]() .
.
【解析】
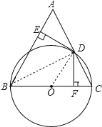
试题分析:(1)连结OD、BD,先根据圆周角定理得到∠BDC=90°,再根据等腰三角形的性质得到AD=CD,则可判断OD为△ABC的中位线,所以OD∥AB,加上DE⊥AB,则DE⊥OD,然后根据切线的判定定理得ED是⊙O的切线;
(2)根据等腰三角形的性质由AB=AC得到∠A=∠C,在Rt△CFD中利用余弦定理得到cosC=![]() =cosA=
=cosA=![]() ,则可设CF=2x,CD=3x,利用勾股定理得到DF=
,则可设CF=2x,CD=3x,利用勾股定理得到DF=![]() x,所以
x,所以![]() x=3
x=3![]() ,解得x=3,于是计算出CD=9,然后在Rt△BCD中利用余弦的定义计算出BC的长即可.
,解得x=3,于是计算出CD=9,然后在Rt△BCD中利用余弦的定义计算出BC的长即可.
试题解析:(1)连结OD、BD,∵BC为直径,∴∠BDC=90°,∴BD⊥AC,
而BA=BC,∴AD=CD,而OB=OC,∴OD为△ABC的中位线,∴OD∥AB,
∵DE⊥AB,∴DE⊥OD,∴ED是⊙O的切线;
(2)∵AB=AC,∴∠A=∠C,在Rt△CFD中,cosC=![]() =cosA=
=cosA=![]() ,
,
设CF=2x,CD=3x,
∴DF=![]() =
=![]() x,∴
x,∴![]() x=3
x=3![]() ,解得x=3,∴CD=9,
,解得x=3,∴CD=9,
在Rt△BCD中,∵cosC=![]() =
=![]() ,∴BC=
,∴BC=![]() ×9=
×9=![]() ,
,
即⊙O的直径为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
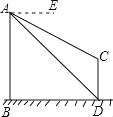
【题目】如图,AB、CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶点A点测得建筑物CD的顶点C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°.
(1)求两建筑物底部之间水平距离BD的长度;
(2)求建筑物CD的高度(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线p:y=ax2+bx+c的顶点为C,与x轴相交于A、B两点(点A在点B左侧),点C关于x轴的对称点为C′,我们称以A为顶点且过点C′,对称轴与y轴平行的抛物线为抛物线p的“梦之星”抛物线,直线AC′为抛物线p的“梦之星”直线.若一条抛物线的“梦之星”抛物线和“梦之星”直线分别是y=x2+2x+1和y=2x+2,则这条抛物线的解析式为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB,DC(或它们的延长线)于点M,N.当∠MAN绕点A旋转到BM=DN时(如图1),易证BM+DN=MN.

(1)当∠MAN绕点A旋转到BM≠DN时(如图2),线段BM,DN和MN之间有怎样的数量关系?写出猜想,并加以证明.
(2)当∠MAN绕点A旋转到如图3的位置时,线段BM,DN和MN之间又有怎样的数量关系?请直接写出你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面网格中每个小正方形的边长为1. 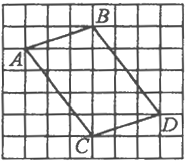
(1)线段CD是线段AB经过怎样的平移后得到的?
(2)线段AC是线段BD经过怎样的平移后得到的?
查看答案和解析>>
科目:初中数学 来源: 题型:
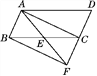
【题目】如图,已知点E是ABCD中BC边的中点,连接AE并延长交DC的延长线于点F.
(1)连接AC,BF,若∠AEC=2∠ABC,求证:四边形ABFC为矩形;
(2)在(1)的条件下,若△AFD是等边三角形,且边长为4,求四边形ABFC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年我国粮食生产首次实现了建国以来的“十连增”,全年粮食产量突破12000亿斤.将1 200 000 000 000用科学记数法表示为( )
A. 12×1011 B. 1.2×1011 C. 1.2×1012 D. 0.12×1013
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出下列4个命题:①对顶角相等;②同位角相等;③在同一个圆中,同一条弦所对的圆周角都相等;④圆的内接四边形对角互补.其中,真命题为( )
A. ①②④B. ①③④C. ①④D. ①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com