
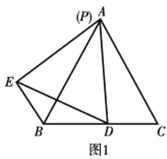
【题目】在等边三角形ABC中,AB=6,点D是BC边上的一点,点P是AB边上的一点,连接PD,以PD为边作等边三角形PDE,连接BE.
(1)如图1,当点P与点A重合时,
①找出图中的一对全等三角形,并证明;
②BE+BD=;
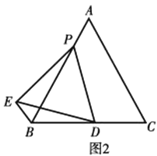
(2)如图2,若AP=1,请计算BE+BD的值.
科目:初中数学 来源: 题型:
【题目】如图,一个半径为r的圆形纸片在边长为a( ![]() )的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“不能接触到的部分”的面积是( )
)的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“不能接触到的部分”的面积是( )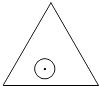
A.![]()
B.![]()
C.![]()
D.πr2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个三角形两边中点的连线叫做这个三角形的中位线.只要顺次连结三角形三条中位线,则可将原三角形分割为四个全等的小三角形(如图(1));把三条边分成三等份,再按照图(2)将分点连起来,可以看作将整个三角形分成9个全等的小三角形;把三条边分成四等份,…,按照这种方式分下去,第n个图形中应该得到( )个全等的小三角形.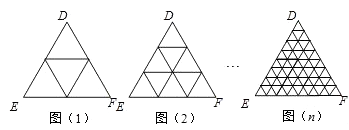
A.![]()
B.![]()
C.![]()
D.(n+1)2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新春佳节来临,某公司组织10辆汽车装运苹果、芦柑、香梨三种水果共60吨去外地销售,要求10辆汽车全部装满,每辆汽车只能装运同一种水果,且装运每种水果的车辆都不少于2辆,根据下表提供的信息,解答以下问题:
苹果 | 芦柑 | 香梨 | |
每辆汽车载货量 | 7 | 6 | 5 |
每车水果获利 | 2500 | 3000 | 2000 |
![]() 设装运苹果的车辆为x辆,装运芦柑的车辆为y辆,求y与x之间的函数关系式,并直接写出x的取值范围
设装运苹果的车辆为x辆,装运芦柑的车辆为y辆,求y与x之间的函数关系式,并直接写出x的取值范围
![]() 用w来表示销售获得的利润,那么怎样安排车辆能使此次销售获利最大?并求出w的最大值.
用w来表示销售获得的利润,那么怎样安排车辆能使此次销售获利最大?并求出w的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=60°,BC=2,CD是△ABC的一条高线.若E,F分别是CD和BC上的动点,则BE+EF的最小值是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c上部分点的横坐标x纵坐标y的对应值如下表,则下列说法中错误的是( ).
x | … | -4 | -3 | -2 | -1 | 0 | 1 | … |
y | … | -37 | -21 | -9 | -1 | 3 | 3 | … |
A.当x>1时y随x的增大而增大
B.抛物线的对称轴为x= ![]()
C.当x=2时y=-1
D.方程ax2+bx+c=0一个负数解x1满足-1<x1<0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】港珠澳大桥是世界最长的跨海大桥,连接香港大屿山、澳门半岛和广东省珠海市,其中珠海站到香港站全长约55千米,2018年10月24日上午9时正式通车.一辆观光巴士自珠海站出发,25分钟后,一辆小汽车从同一地点出发,结果同时到达香港站.已知小汽车的速度是观光巴士的1.6倍,求观光巴士的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个小组同时从山脚开始攀登一座600m高的山,第一小组的攀登速度(即攀登高度与攀登时间之比)是第二小组的1.2倍,并比第二小组早20min到达山顶.
(1)第二小组的攀登速度是多少?
(2)如果山高为hm,第一小组的攀登速度是第二小组的k(k>1)倍,并比第二小组早tmin到达山顶,则第一小组的攀登速度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果a c b ,那么我们规定(a,b)=c,例如:因为23 8 ,所以(2,8)=3.
(1)根据上述规定,填空:(3,27)= ,(4,1)= ,(2,![]() )= ;
)= ;
(2)若记(3,5)=a,(3,6)=b,(3,30)=c,求证: a b c .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com