练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如果a c b ，那么我们规定（a，b）=c，例如：因为23 8 ，所以（2，8）=3．

    （1）根据上述规定，填空：（3，27）= ，（4，1）= ，（2， ）= ；

    （2）若记（3，5）=a，（3，6）=b，（3，30）=c，求证： a b c ．

    【答案】（1）3；0； 2；（2）证明见解析.

    【解析】

    （1）根据已知和同底数的幂法则得出即可；

    （2）根据已知得出3a=5，3b=6，3c=30，求出3a×3b=30，即可得出答案．

    （1）（3，27）=3，（4，1）=0，（2，）=-2，

    故答案为3；0；-2；

    （2）证明：由题意得：3a 5，3b 6，3c 30，

    ∵ 5 6=30，

    ∴ 3a 3b 3c，

    ∴ 3ab 3c，

    ∴ a b c．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

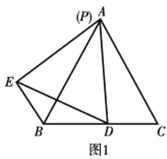
    【题目】在等边三角形ABC中，AB=6，点D是BC边上的一点，点P是AB边上的一点，连接PD，以PD为边作等边三角形PDE，连接BE．

    （1）如图1，当点P与点A重合时，

    ①找出图中的一对全等三角形，并证明；

    ②BE+BD=；

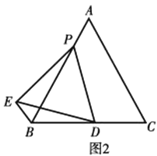
    （2）如图2，若AP=1，请计算BE+BD的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某公司生产一种新型生物医药产品，生产成本为2万元/ 吨，每月生产能力为12吨，且生产出的产品都能销售出去.这种产品部分内销，另一部分外销（出口），内销与外销的单价 （单位：万元/吨）与销量的关系分别如图1，图2.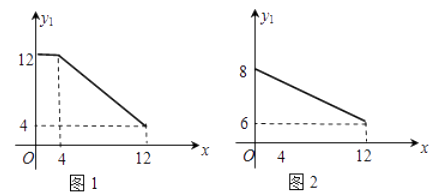

    （1）如果该公司内销数量为x（单位：吨），内、外销单价分别为y 1 , y 2 ,求, 关于x的函数解析式；
    （2）如果该公司内销数量为x（单位：吨），求内销获得的毛利润 关于x的函数解析式；
    （3）请设计一种销售方案，使该公司本月能获得最大毛利润，并求出毛利润的最大值.（毛利润=销售收入－生产成本）.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB是⊙O的直径，C是半圆O上的一点，AC平分∠DAB,AD CD,垂足为D，AD交⊙O 于E,连接CE.

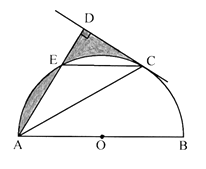
    （1）求证：CD 是⊙O 的切线
    （2）若E是弧AC的中点，⊙O 的半径为1，求图中阴影部分的面积。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，在△ABC中，AD⊥BC于D，CE⊥AB于E，AD与CE交于点F，且AD=CD．

    （1）求证：△ABD≌△CFD；

    （2）已知BC=7，AD=5，求AF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了更好改善河流的水质，治污公司决定购买10台污水处理设备．现有A，B两种型号的设备，经过市场调查，购买一台型设备比购买一台型设备多花费2万元，购买2台A型设备比购买3台B型设备少花费6万元．

    （1）购买一台A型设备、购买一台B型设备各需要多少万元；

    （2）治污公司经预算购买污水处理设备的资金不超过105万元，你认为该公司有哪几种购买方案．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在如图所示的正方形网格中，每个小正方形的边长为1，格点三角形（顶点是网格线的交点的三角形）ABC的顶点A，C的坐标分别为（﹣4，5），（﹣1，3）．

    （1）在如图所示的网格平面内作出平面直角坐标系；

    （2）作出△ABC关于y轴对称的△A′B′C′，并写出点B′的坐标；

    （3）P是x轴上的动点，在图中找出使△A′BP周长最短时的点P，直接写出点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，点C在线段AB上，（点C不与A、B重合），分别以AC、BC为边在AB同侧作等边三角形ACD和等边三角形BCE，连接AE、BD交于点P．

    （观察猜想）

    ①AE与BD的数量关系是　 　；

    ②∠APD的度数为　 　．

    （数学思考）

    如图2，当点C在线段AB外时，（1）中的结论①、②是否仍然成立？若成立，请给予证明；若不成立，请你写出正确结论再给予证明；

    （拓展应用）

    如图3，点E为四边形ABCD内一点，且满足∠AED＝∠BEC＝90°，AE＝DE，BE＝CE，对角线AC、BD交于点P，AC＝10，则四边形ABCD的面积为　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】完成推理过程

    （1）如图，已知∠1=∠2，∠B=∠C，求证：AB∥CD．

    证明∵∠1=∠2(已知)，

    且∠1=∠CGD(　　)

    ∴∠2=∠CGD( 　　　　)，

    ∴CE∥BF(　　)，

    ∴∠C=∠BFD(　　)

    又∵∠B=∠C(已知)，

    ∴∠BFD=∠B(　　)，

    ∴AB∥CD(　　)

    查看答案和解析>>

    同步练习册答案