
【题目】如图1,点C在线段AB上,(点C不与A、B重合),分别以AC、BC为边在AB同侧作等边三角形ACD和等边三角形BCE,连接AE、BD交于点P.
(观察猜想)
①AE与BD的数量关系是 ;
②∠APD的度数为 .
(数学思考)
如图2,当点C在线段AB外时,(1)中的结论①、②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明;
(拓展应用)
如图3,点E为四边形ABCD内一点,且满足∠AED=∠BEC=90°,AE=DE,BE=CE,对角线AC、BD交于点P,AC=10,则四边形ABCD的面积为 .

【答案】【观察猜想】:①AE=BD.②∠APD=60°.理由见解析;【数学思考】:结论仍然成立,证明见解析;【拓展应用】:50.
【解析】
观察猜想:证明△ACE≌△DCB(SAS),可得AE=BD,∠CAO=∠ODP,由∠AOC=∠DOP,推出∠DPO=∠ACO=60°;
数学思考:结论成立,证明方法类似;
拓展应用:证明AC⊥BD,可得S四边形ABCD=![]() ACDP+
ACDP+![]() ACPB=
ACPB=![]() AC(DP+PB)=
AC(DP+PB)=![]() ACBD.
ACBD.
观察猜想:结论:AE=BD.∠APD=60°.
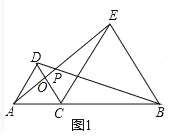
理由:设AE交CD于点O.
∵△ADC,△ECB都是等边三角形,
∴CA=CD,∠ACD=∠ECB=60°,CE=CB,
∴∠ACE=∠DCB,
∴△ACE≌△DCB(SAS),
∴AE=BD,∠CAO=∠ODP,
∵∠AOC=∠DOP,
∴∠DPO=∠ACO=60°,
即∠APD=60°.
故答案为AE=BD,60°.
数学思考:结论仍然成立.
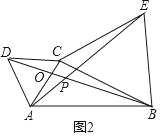
理由:设AC交BD于点O.
∵△ADC,△ECB都是等边三角形,
∴CA=CD,∠ACD=∠ECB=60°,CE=CB,
∴∠ACE=∠DCB
∴△ACE≌△DCB(SAS),
∴AE=BD,∠PAO=∠ODC,
∵∠AOP=∠DOC,
∴∠APO=∠DCO=60°,
即∠APD=60°.
拓展应用:
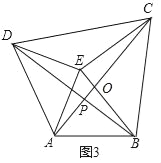
设AC交BE于点O.
∵△ADE,△ECB都是等腰直角三角形,
∴ED=EA,∠AED=∠BEC=90°,CE=EB,
∴∠AEC=∠DEB
∴△AEC≌△DEB(SAS),
∴AC=BD=10,∠PBO=∠OCE,
∵∠BOP=∠EOC,
∴∠BPO=∠CEO=90°,
∴AC⊥BD,
∴S四边形ABCD=![]() ACDP+
ACDP+![]() ACPB=
ACPB=![]() AC(DP+PB)=
AC(DP+PB)=![]() ACBD=50.
ACBD=50.
故答案为:50.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】两个小组同时从山脚开始攀登一座600m高的山,第一小组的攀登速度(即攀登高度与攀登时间之比)是第二小组的1.2倍,并比第二小组早20min到达山顶.
(1)第二小组的攀登速度是多少?
(2)如果山高为hm,第一小组的攀登速度是第二小组的k(k>1)倍,并比第二小组早tmin到达山顶,则第一小组的攀登速度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果a c b ,那么我们规定(a,b)=c,例如:因为23 8 ,所以(2,8)=3.
(1)根据上述规定,填空:(3,27)= ,(4,1)= ,(2,![]() )= ;
)= ;
(2)若记(3,5)=a,(3,6)=b,(3,30)=c,求证: a b c .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学在学习多项式乘以多项式时发现:(![]() x+6)(2x+3)(5x﹣4)的结果是一个多项式,并且最高次项为:
x+6)(2x+3)(5x﹣4)的结果是一个多项式,并且最高次项为:![]() x2x5x=5x3,常数项为:6×3×(﹣4)=﹣72,那么一次项是多少呢?要解决这个问题,就是要确定该一次项的系数.根据尝试和总结他发现:一次项系数就是:×3×(﹣4)+2×(﹣4)×6+5×6×3=36,即一次项为36x.认真领会小明同学解决问题的思路,方法,仔细分析上面等式的结构特征.结合自己对多项式乘法法则的理解,解决以下问题.
x2x5x=5x3,常数项为:6×3×(﹣4)=﹣72,那么一次项是多少呢?要解决这个问题,就是要确定该一次项的系数.根据尝试和总结他发现:一次项系数就是:×3×(﹣4)+2×(﹣4)×6+5×6×3=36,即一次项为36x.认真领会小明同学解决问题的思路,方法,仔细分析上面等式的结构特征.结合自己对多项式乘法法则的理解,解决以下问题.
(1)计算(x+1)(3x+2)(4x﹣3)所得多项式的一次项系数为 .
(2)(![]() x+6)(2x+3)(5x﹣4)所得多项式的二次项系数为 .
x+6)(2x+3)(5x﹣4)所得多项式的二次项系数为 .
(3)若计算(x2+x+1)(x2﹣3x+a)(2x﹣1)所所得多项式的一次项系数为0,则a= .
(4)若(x+1)2018=a0x2018+a1x2017+a2x2016+a3x2015…+a2017x++a2018,则a2017= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠XOY=90°,点A、B分别在射线OX、OY上移动(不与点O重合),BE是∠ABY的平分线,BE的反向延长线与∠OAB的平分线相交于点C.
(1)当∠OAB=40°时,∠ACB= 度;
(2)随点A、B的移动,试问∠ACB的大小是否变化?如果保持不变,请给出证明;如果发生变化,请求出变化范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,AB∥CD,∠A=38°,∠C=50°,求∠APC的度数.(提示:作PE∥AB).
(2)如图2,AB∥DC,当点P在线段BD上运动时,∠BAP=∠α,∠DCP=∠β,求∠CPA与∠α,∠β之间的数量关系,并说明理由.
(3)在(2)的条件下,如果点P在段线OB上运动,请你直接写出∠CPA与∠α,∠β之间的数量关系______.
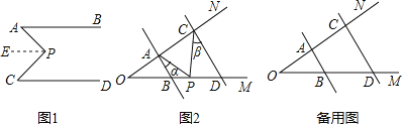
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次课外实践活动中,同学们要测量某公园人工湖两侧A,B两个凉亭之间的距离.现测得AC=50m,BC=100m,∠CAB=120°,请计算A,B两个凉亭之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某童装店有A、B两种型号的童装,其进价与售价如下表所示:
型号 | 进价(元) | 售价(元) |
A型 | 90 | 108 |
B型 | 100 | 130 |
根据市场需要,服装店决定:购进A种服装的数量要比购进B种服装的2倍还多4件,且A种服装购进数量不超过28件,并使这批服装全部销售完毕后的总利润不少于699元.若假设购进B种服装x件,那么:
(1)请写出A、B两种服装全部销售完毕后的总利润y/元用含x/件的式子表示;
(2)请问该服装店有几种满足条件的进货方案?哪种方案获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义符号min{a,b}的含义为:当a≥b时,min{a,b}=b;当a<b时,min{a,b}=a.如:min{1,﹣2}=﹣2,min{﹣1,2}=﹣1.
(1)求min{x2﹣1,﹣2};
(2)已知min{x2﹣2x+k,﹣3}=﹣3,求实数k的取值范围;
(3)已知当﹣2≤x≤3时,min{x2﹣2x﹣15,m(x+1)}=x2﹣2x﹣15.直接写出实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com