
【题目】定义符号min{a,b}的含义为:当a≥b时,min{a,b}=b;当a<b时,min{a,b}=a.如:min{1,﹣2}=﹣2,min{﹣1,2}=﹣1.
(1)求min{x2﹣1,﹣2};
(2)已知min{x2﹣2x+k,﹣3}=﹣3,求实数k的取值范围;
(3)已知当﹣2≤x≤3时,min{x2﹣2x﹣15,m(x+1)}=x2﹣2x﹣15.直接写出实数m的取值范围.
【答案】
(1)解:∵x2≥0,
∴x2﹣1≥﹣1,
∴x2﹣1>﹣2.
∴min{x2﹣1,﹣2}=﹣2,
(2)解:∵x2﹣2x+k=(x﹣1)2+k﹣1,
∴(x﹣1)2+k﹣1≥k﹣1.
∵min{x2﹣2x+k,﹣3}=﹣3,
∴k﹣1≥﹣3.
∴k≥﹣2,
(3)解:对于y=x2﹣2x﹣15,当x=﹣2时,y=﹣7,
当x=3时,y=﹣12,
由题意可知抛物线y=x2﹣2x﹣15与直线y=m(x+1)的交点坐标为(﹣2,﹣7),(3,﹣12),
所以m的范围是:﹣3≤m≤7.
【解析】(1)根据平方的非负性得出x2≥0,然后根据不等式的性质1得出x2﹣1≥﹣1,从而判断出x2﹣1>﹣2,根据新定义得出结论;
(2)将代数式x2﹣2x+k配方变形成(x﹣1)2+k﹣1,根据平方的非负性得出(x﹣1)2![]() 0,进而得出(x﹣1)2+k﹣1≥k﹣1,再根据min{x2﹣2x+k,﹣3}=﹣3,从而得出不等式k﹣1≥﹣3,解不等式即可;
0,进而得出(x﹣1)2+k﹣1≥k﹣1,再根据min{x2﹣2x+k,﹣3}=﹣3,从而得出不等式k﹣1≥﹣3,解不等式即可;
(3)把两个界点x=-2与x=3分别代入函数y=x2﹣2x﹣15得出对应的函数值,从而知当﹣2≤x≤3时,min{x2﹣2x﹣15,m(x+1)}=x2﹣2x﹣15时,抛物线y=x2﹣2x﹣15与直线y=m(x+1)的交点坐标为(﹣2,﹣7),(3,﹣12),从而得出m的取值范围。
【考点精析】本题主要考查了一次函数的性质和一元一次不等式的解法的相关知识点,需要掌握一般地,一次函数y=kx+b有下列性质:(1)当k>0时,y随x的增大而增大(2)当k<0时,y随x的增大而减小;步骤:①去分母;②去括号;③移项;④合并同类项; ⑤系数化为1(特别要注意不等号方向改变的问题)才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图1,点C在线段AB上,(点C不与A、B重合),分别以AC、BC为边在AB同侧作等边三角形ACD和等边三角形BCE,连接AE、BD交于点P.
(观察猜想)
①AE与BD的数量关系是 ;
②∠APD的度数为 .
(数学思考)
如图2,当点C在线段AB外时,(1)中的结论①、②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明;
(拓展应用)
如图3,点E为四边形ABCD内一点,且满足∠AED=∠BEC=90°,AE=DE,BE=CE,对角线AC、BD交于点P,AC=10,则四边形ABCD的面积为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成推理过程
(1)如图,已知∠1=∠2,∠B=∠C,求证:AB∥CD.
证明∵∠1=∠2(已知),
且∠1=∠CGD( )
∴∠2=∠CGD( ),
∴CE∥BF( ),
∴∠C=∠BFD( )
又∵∠B=∠C(已知),
∴∠BFD=∠B( ),
∴AB∥CD( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=60°,∠ABC=45°,AB= ![]() ,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB、AC于E、F,连接EF,则线段EF长度的最小值为 .
,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB、AC于E、F,连接EF,则线段EF长度的最小值为 . 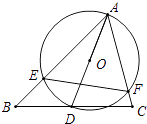
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B两地被池塘隔开,小明通过下列方法测出了A、B间的距离:先在AB外选一点C,然后测出AC,BC的中点M,N,并测量出MN的长为6 m,由此他就知道了A、B间的距离.有关他这次探究活动的描述错误的是

A. AB=12 m B. MN∥AB
C. △CMN∽△CAB D. CM∶MA=1∶2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在Rt△ABC中,∠C=90°,点D是AC的中点,且∠A+∠CDB=90°,过点A、D作⊙O,使圆心O在AB上,⊙O与AB交于点E.
(1)求证:直线BD与⊙O相切;
(2)若AD:AE=4:5,BC=6,求⊙O的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,铜亭广场装有智能路灯,路灯设备由灯柱AC与支架BD共同组成(点C处装有安全监控,点D处装有照明灯),灯柱AC为6米,支架BD为2米,支点B到A的距离为4米,AC与地面垂直,∠CBD=60°.某一时刻,太阳光与地面的夹角为45°,求此刻路灯设备在地面上的影长为多少?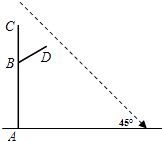
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com