
【题目】如图1,矩形ABCD中,E是AD的中点,以点E直角顶点的直角三角形EFG的两边EF,EG分别过点B,C,∠F=30°.
(1)求证:BE=CE
(2)将△EFG绕点E按顺时针方向旋转,当旋转到EF与AD重合时停止转动.若EF,EG分别与AB,BC相交于点M,N.(如图2)
①求证:△BEM≌△CEN;
②若AB=2,求△BMN面积的最大值;
③当旋转停止时,点B恰好在FG上(如图3),求sin∠EBG的值.



【答案】(1)详见解析;(2)①详见解析;②2;③![]() .
.
【解析】
(1)只要证明△BAE≌△CDE即可;
(2)①利用(1)可知△EBC是等腰直角三角形,根据ASA即可证明;
②构建二次函数,利用二次函数的性质即可解决问题;
③如图3中,作EH⊥BG于H.设NG=m,则BG=2m,BN=EN=![]() m,EB=
m,EB=![]() m.利用面积法求出EH,根据三角函数的定义即可解决问题.
m.利用面积法求出EH,根据三角函数的定义即可解决问题.
(1)证明:如图1中,
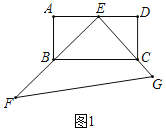
∵四边形ABCD是矩形,
∴AB=DC,∠A=∠D=90°,
∵E是AD中点,
∴AE=DE,
∴△BAE≌△CDE,
∴BE=CE.
(2)①解:如图2中,

由(1)可知,△EBC是等腰直角三角形,
∴∠EBC=∠ECB=45°,
∵∠ABC=∠BCD=90°,
∴∠EBM=∠ECN=45°,
∵∠MEN=∠BEC=90°,
∴∠BEM=∠CEN,
∵EB=EC,
∴△BEM≌△CEN;
②∵△BEM≌△CEN,
∴BM=CN,设BM=CN=x,则BN=4-x,
∴S△BMN=![]() x(4-x)=-
x(4-x)=-![]() (x-2)2+2,
(x-2)2+2,
∵-![]() <0,
<0,
∴x=2时,△BMN的面积最大,最大值为2.
③解:如图3中,作EH⊥BG于H.设NG=m,则BG=2m,BN=EN=![]() m,EB=
m,EB=![]() m.
m.

∴EG=m+![]() m=(1+
m=(1+![]() )m,
)m,
∵S△BEG=![]() EGBN=
EGBN=![]() BGEH,
BGEH,
∴EH=![]() =
=![]() m,
m,
在Rt△EBH中,sin∠EBH=![]() .
.


科目:初中数学 来源: 题型:
【题目】(1)如图①,AD是△ABC的中线.△ABD与△ACD的面积有怎样的数量关系?为什么?

(2)若三角形的面积记为S,例如:△ABC的面积记为S△ABC.如图②,已知S△ABC=1.△ABC的中线AD、CE相交于点O,求四边形BDOE的面积.

小华利用(1)的结论,解决了上述问题,解法如下:
连接BO,设S△BEO=x,S△BDO=y,由(1)结论可得:S△BCE=S△BAD=![]() S△ABC=
S△ABC=![]() ,S△BCO=2S△BDO=2y,S△BAO=2S△BEO=2x.则有
,S△BCO=2S△BDO=2y,S△BAO=2S△BEO=2x.则有 即
即 所以x+y=
所以x+y=![]() .即四边形BDOE面积为
.即四边形BDOE面积为![]() .
.
请仿照上面的方法,解决下列问题:
①如图③,已知S△ABC=1.D、E是BC边上的三等分点,F、G是AB边上的三等分点,AD、CF交于点O,求四边形BDOF的面积.

②如图④,已知S△ABC=1.D、E、F是BC边上的四等分点,G、H、I是AB边上的四等分点,AD、CG交于点O,则四边形BDOG的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C在一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD,BD于点M,P,CD交BE于点Q,连接PQ,BM,下面结论:
①△ABE≌△DBC;②∠DMA=60°;③△BPQ为等边三角形;④MB平分∠AMC,
其中结论正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形ABCD各顶点的坐标分别为A(0,1)、B(5,1)、C(7,3)、D(2,5).
(1)填空:四边形ABCD内(边界点除外)一共有 个整点(即横坐标和纵坐标都是整数的点);
(2)求四边形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年湖南省进入高中学习的学生三年后将面对新高考,高考方案与高校招生政策都将有重大变化。某部门为了了解政策的宣传情况,对某初级中学学生进行了随机抽样调查,根据学生对政策的了解程度由高到低分为A,B,C,D四个等级,并对调查结果分析后绘制了如下两幅图不完整的统计图。请你根据图中提供的信息完成下列问题:
(1)求被调查学生的人数,并将条形统计图补充完整;
(2)求扇形统计图中的A等对应的扇形圆心角的度数;
(3)已知该校有1500名学生,估计该校学生对政策内容了解程度达到A等的学生有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰三角形ABC中,∠ABC=90°,D为AC边上中点,过D点作DE⊥DF交AB于E,交BC于F,若四边形BFDE的面积为16,则AB的长为( )

A.8B.10C.12D.16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB边的垂直平分线l1交BC于点D,AC边的垂直平分线l2交BC于点E,l1与l2相交于点O,连接AD,AE,△ADE的周长为12cm.
(1)求BC的长;
(2)分别连接OA,OB,OC,若△OBC的周长为26cm,求OA的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一位篮球运动员在距离篮圈中心水平距离4m处起跳投篮,球沿一条抛物线运动,当球运动的水平距离为2.5m时,达到最大高度3.5m,然后准确落入篮框内.已知篮圈中心距离地面高度为3.05m,在如图所示的平面直角坐标系中,下列说法正确的是( )
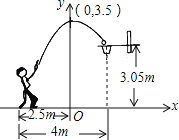
A. 此抛物线的解析式是y=﹣![]() x2+3.5
x2+3.5
B. 篮圈中心的坐标是(4,3.05)
C. 此抛物线的顶点坐标是(3.5,0)
D. 篮球出手时离地面的高度是2m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程ax+b=0(a≠0)的解为x=-2,点(1,3)是抛物线y=ax2+bx+c(a≠0)上的一个点,则下列四个点中一定在该抛物线上的是( )
A. (2,3) B. (0,3)
C. (-1,3) D. (-3,3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com