
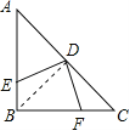
【题目】如图,在等腰三角形ABC中,∠ABC=90°,D为AC边上中点,过D点作DE⊥DF交AB于E,交BC于F,若四边形BFDE的面积为16,则AB的长为( )

A.8B.10C.12D.16
【答案】A
【解析】
连接BD,根据等腰直角三角形的性质可得BD=CD,∠C=∠ABD=45°,根据直角三角形两锐角互余的关系可得∠FDC=∠EDB,利用ASA可证明△EDB≌△FDC,可得S四边形BFDE=S△BDC=![]() S△ABC,根据三角形面积公式求出AB的长即可得答案.
S△ABC,根据三角形面积公式求出AB的长即可得答案.
连接BD,
∵等腰三角形ABC中,∠ABC=90°,
∴△ABC是等腰直角三角形,
∴∠C=45°,
∵D为AC边上中点,
∴BD⊥AC(三线合一),BD=CD=AD,∠ABD=45°,
∴∠ABD=∠C,
又∵DE⊥DF,
∴∠FDC+∠BDF=∠EDB+∠BDF=90°,
∴∠FDC=∠EDB,
在△EDB与△FDC中,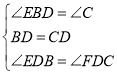 ,
,
∴△EDB≌△FDC(ASA),
∴S四边形BFDE=S△BDC=![]() S△ABC=16,
S△ABC=16,
∴![]() AB2=32,
AB2=32,
∴AB=8,
故选A.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,将
,将![]() 沿直线
沿直线![]() 向右平移2个单位得到
向右平移2个单位得到![]() ,连接
,连接![]() ,则下列结论:①
,则下列结论:①![]() ,
,![]() ;②
;②![]() ;③四边形
;③四边形![]() 的周长是16;④S四边形ABEO=S四边形CFDO其中结论正确的个数有( )
的周长是16;④S四边形ABEO=S四边形CFDO其中结论正确的个数有( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某民营企业准备用14000元从外地购进A、B两种商品共600件,其中A种商品的成本价为20元,B种商品的成本价为30元.
(1)该民营企业从外地购得A、B两种商品各多少件?
(2)该民营企业计划租用甲、乙两种货车共6辆,一次性将A、B两种商品运往某城市,已知每辆甲种货车最多可装A种商品110件和B种商品20件;每辆乙种货车最多可装A种商品30件和B种商品90件,问安排甲、乙两种货车有几种方案?请你设计出具体的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,矩形ABCD中,E是AD的中点,以点E直角顶点的直角三角形EFG的两边EF,EG分别过点B,C,∠F=30°.
(1)求证:BE=CE
(2)将△EFG绕点E按顺时针方向旋转,当旋转到EF与AD重合时停止转动.若EF,EG分别与AB,BC相交于点M,N.(如图2)
①求证:△BEM≌△CEN;
②若AB=2,求△BMN面积的最大值;
③当旋转停止时,点B恰好在FG上(如图3),求sin∠EBG的值.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了检验教室里的矩形门框是否合格,某班的四个学习小组用三角板和细绳分别测得如下结果,其中不能判定门框是否合格的是( )
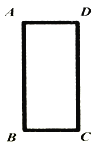
A. AB=CD,AD=BC,AC=BD B. AC=BD,∠B=∠C=90° C. AB=CD,∠B=∠C=90° D. AB=CD,AC=BD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,DF∥AC,E点为DF上的点,B为AC上的点,∠1=∠2.求证:∠C=∠D.请你根据条件进行推理,得出结论,并在括号内注明原因.

证明:∵∠1=∠2(已知)
∠1=∠3,∠2=∠4(_______),
∴∠3=∠4(等量代换),
∴_____∥_____(_______),
∴∠C=∠ABD(_______),
∵DF∥AC(已知)
∴∠D=∠ABD(_______),
∴∠C=∠D(_______).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com