
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,将
,将![]() 沿直线
沿直线![]() 向右平移2个单位得到
向右平移2个单位得到![]() ,连接
,连接![]() ,则下列结论:①
,则下列结论:①![]() ,
,![]() ;②
;②![]() ;③四边形
;③四边形![]() 的周长是16;④S四边形ABEO=S四边形CFDO其中结论正确的个数有( )
的周长是16;④S四边形ABEO=S四边形CFDO其中结论正确的个数有( )

A.1个B.2个C.3个D.4个
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,∠ABC ∠ACB ,BD 、CD 分别平分△ABC 的内角 ∠ABC 、外角 ∠ACP ,BE平分外角 ∠MBC 交 DC 的延长线于点 E ,以下结论:①∠BDE ![]() ∠BAC ;② DB⊥BE ;③∠BDC ∠ACB 90 ;④∠BAC 2∠BEC 180 .其中正确的结论有( )
∠BAC ;② DB⊥BE ;③∠BDC ∠ACB 90 ;④∠BAC 2∠BEC 180 .其中正确的结论有( )
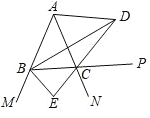
A.1 个B.2 个C.3 个D.4 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B、C在数轴上分别表示的数为-10,2,8,点D是BC中点,点E是AD中点.
(1)求EB的长;
(2)若动点P从点A出发,以1cm/s的速度向点C运动,达到点C停止运动,点Q从点C出发,以2cm/s的速度向点A运动,到达点A停止运动,若运动时间为ts,当t为何值时,PQ=3cm?
(3)点A,B,C开始在数轴上运动,若点A以1cm/s的速度向左运动,同时,点B和点C分别以4cm/s和9cm/s的速度向右运动,假设t秒钟过后,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB,请问:AB-BC的值是否随时间t的变化而变化?若变化,请说明理由;若不变,请求其常数值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富同学们的课余生活,某学校将举行“亲近大自然”户外活动.现随机抽取了部分学生进行主题为“你最想去的景点是”的问卷调查,要求学生只能从“A(世博园),B(劳动公园),C(月牙岛公园),D(赫图阿拉城)”四个景点中选择一项,根据调查结果,绘制了如下两幅不完整的统计图:

(1)本次共调查了多少名学生?
(2)补全条形统计图;
(3)在扇形统计图中,求B(劳动公园)部分所占的圆心角度数;
(4)若该学校共有3600名学生,试估计该校最想去月牙岛公园的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,AD是△ABC的中线.△ABD与△ACD的面积有怎样的数量关系?为什么?

(2)若三角形的面积记为S,例如:△ABC的面积记为S△ABC.如图②,已知S△ABC=1.△ABC的中线AD、CE相交于点O,求四边形BDOE的面积.

小华利用(1)的结论,解决了上述问题,解法如下:
连接BO,设S△BEO=x,S△BDO=y,由(1)结论可得:S△BCE=S△BAD=![]() S△ABC=
S△ABC=![]() ,S△BCO=2S△BDO=2y,S△BAO=2S△BEO=2x.则有
,S△BCO=2S△BDO=2y,S△BAO=2S△BEO=2x.则有 即
即 所以x+y=
所以x+y=![]() .即四边形BDOE面积为
.即四边形BDOE面积为![]() .
.
请仿照上面的方法,解决下列问题:
①如图③,已知S△ABC=1.D、E是BC边上的三等分点,F、G是AB边上的三等分点,AD、CF交于点O,求四边形BDOF的面积.

②如图④,已知S△ABC=1.D、E、F是BC边上的四等分点,G、H、I是AB边上的四等分点,AD、CG交于点O,则四边形BDOG的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为2的正△ABC的边BC在直线l上,两条距离为l的平行直线a和b垂直于直线l,a和b同时向右移动(a的起始位置在B点),速度均为每秒1个单位,运动时间为t(秒),直到b到达C点停止,在a和b向右移动的过程中,记△ABC夹在a和b之间的部分的面积为s,则s关于t的函数图象大致为( )

A.  B.
B.  C.
C. 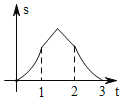 D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰三角形ABC中,∠ABC=90°,D为AC边上中点,过D点作DE⊥DF交AB于E,交BC于F,若四边形BFDE的面积为16,则AB的长为( )

A.8B.10C.12D.16
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com