
【题目】如图,正方形ABCD的边长为2a,E为BC边的中点,![]() 的圆心分别在边AB、CD上,这两段圆弧在正方形内交于点F,则E、F间的距离为 .
的圆心分别在边AB、CD上,这两段圆弧在正方形内交于点F,则E、F间的距离为 .
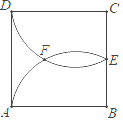
【答案】![]() a.
a.
【解析】
作DE的中垂线交CD于G,则G为![]() 的圆心,H为
的圆心,H为![]() 的圆心,连接EF,GH,交于点O,连接GF,FH,HE,EG,依据勾股定理可得GE=FG=
的圆心,连接EF,GH,交于点O,连接GF,FH,HE,EG,依据勾股定理可得GE=FG=![]() a,根据四边形EGFH是菱形,四边形BCGH是矩形,即可得到Rt△OEG中,OE=
a,根据四边形EGFH是菱形,四边形BCGH是矩形,即可得到Rt△OEG中,OE=![]() a,即可得到EF=
a,即可得到EF=![]() a.
a.
如图,作DE的中垂线交CD于G,则G为![]() 的圆心,同理可得,H为
的圆心,同理可得,H为![]() 的圆心,
的圆心,
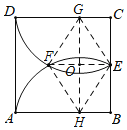
连接EF,GH,交于点O,连接GF,FH,HE,EG,
设GE=GD=x,则CG=2a-x,CE=a,
Rt△CEG中,(2a-x)2+a2=x2,
解得x=![]() a,
a,
∴GE=FG=![]() a,
a,
同理可得,EH=FH=![]() a,
a,
∴四边形EGFH是菱形,四边形BCGH是矩形,
∴GO=![]() BC=a,
BC=a,
∴Rt△OEG中,OE=![]() ,
,
∴EF=![]() a,
a,
故答案为:![]() a.
a.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,已知AB=BC=CA=4cm,AD⊥BC于D,点P、Q分别从B、C两点同时出发,其中点P沿BC向终点C运动,速度为1cm/s;点Q沿CA、AB向终点B运动,速度为2cm/s,设它们运动的时间为x(s).
(1)求x为何值时,PQ⊥AC;
(2)设△PQD的面积为y(cm2),当0<x<2时,求y与x的函数关系式;
(3)当0<x<2时,求证:AD平分△PQD的面积;
(4)探索以PQ为直径的圆与AC的位置关系,请写出相应位置关系的x的取值范围(不要求写出过程).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线MN∥PQ,直线AB分别与MN,PQ相交于点A,B.小宇同学利用尺规按以下步骤作图:①以点A为圆心,以任意长为半径作弧交AN于点C,交AB于点D;②分别以C,D为圆心,以大于![]() CD长为半径作弧,两弧在∠NAB内交于点E;③作射线AE交PQ于点F.若AB=2,∠ABP=60°,则线段AF的长为_____.
CD长为半径作弧,两弧在∠NAB内交于点E;③作射线AE交PQ于点F.若AB=2,∠ABP=60°,则线段AF的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,将
,将![]() 沿直线
沿直线![]() 向右平移2个单位得到
向右平移2个单位得到![]() ,连接
,连接![]() ,则下列结论:①
,则下列结论:①![]() ,
,![]() ;②
;②![]() ;③四边形
;③四边形![]() 的周长是16;④S四边形ABEO=S四边形CFDO其中结论正确的个数有( )
的周长是16;④S四边形ABEO=S四边形CFDO其中结论正确的个数有( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图在△ABC中,AD、BE分别是BC,AC边上的高,AD、BE交于H,DA=DB,BH=AC,点F为BH的中点,∠ABE=15°.
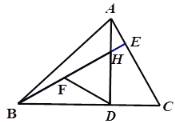
(1)求证:△ADC≌△BDH
(2)求证:DC=DF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在小水池旁有一盏路灯,已知支架AB的长是0.8m,A端到地面的距离AC是4m,支架AB与灯柱AC的夹角为65°.小明在水池的外沿D测得支架B端的仰角是45°,在水池的内沿E测得支架A端的仰角是50°(点C、E、D在同一直线上),求小水池的宽DE.(结果精确到0.1m)(sin65°≈0.9,cos65°≈0.4,tan50°≈1.2)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,以B为圆心,BC长为半径画弧,分别交AC、AB于D、E两点,并连接BD、DE,若∠A=30°,AB=AC,则∠BDE=______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了检验教室里的矩形门框是否合格,某班的四个学习小组用三角板和细绳分别测得如下结果,其中不能判定门框是否合格的是( )
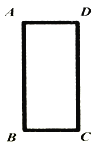
A. AB=CD,AD=BC,AC=BD B. AC=BD,∠B=∠C=90° C. AB=CD,∠B=∠C=90° D. AB=CD,AC=BD
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com