
【题目】△ABC中,以B为圆心,BC长为半径画弧,分别交AC、AB于D、E两点,并连接BD、DE,若∠A=30°,AB=AC,则∠BDE=______.

科目:初中数学 来源: 题型:
【题目】阅读材料并把解答过程补充完整.
问题:在关于x,y的二元一次方程组![]() 中,x>1,y<0,求a的取值范围.
中,x>1,y<0,求a的取值范围.
在关于x,y的二元一次方程组中,利用参数a的代数式表示x,y,然后根据x>1,y<0列出关于参数a的不等式组即可求得a的取值范围.
解:由![]() ,解得
,解得 ,又因为x>1,y<0,所以
,又因为x>1,y<0,所以 ,解得________.
,解得________.
请你按照上述方法,完成下列问题:
已知x-y=4,x>3,y<1,求x+y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,AD是△ABC的中线.△ABD与△ACD的面积有怎样的数量关系?为什么?

(2)若三角形的面积记为S,例如:△ABC的面积记为S△ABC.如图②,已知S△ABC=1.△ABC的中线AD、CE相交于点O,求四边形BDOE的面积.

小华利用(1)的结论,解决了上述问题,解法如下:
连接BO,设S△BEO=x,S△BDO=y,由(1)结论可得:S△BCE=S△BAD=![]() S△ABC=
S△ABC=![]() ,S△BCO=2S△BDO=2y,S△BAO=2S△BEO=2x.则有
,S△BCO=2S△BDO=2y,S△BAO=2S△BEO=2x.则有 即
即 所以x+y=
所以x+y=![]() .即四边形BDOE面积为
.即四边形BDOE面积为![]() .
.
请仿照上面的方法,解决下列问题:
①如图③,已知S△ABC=1.D、E是BC边上的三等分点,F、G是AB边上的三等分点,AD、CF交于点O,求四边形BDOF的面积.

②如图④,已知S△ABC=1.D、E、F是BC边上的四等分点,G、H、I是AB边上的四等分点,AD、CG交于点O,则四边形BDOG的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:直线l:y=2kx-4k+3(k≠0)恒过某一定点P.
(1)求该定点P的坐标;
(2)已知点A、B坐标分别为(0,1)、(2,1),若直线l与线段AB相交,求k的取值范围;
(3)在0≤x≤2范围内,任取3个自变量x1,x2、x3,它们对应的函数值分别为y1、y2、y3,若以y1、y2、y3为长度的3条线段能围成三角形,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C在一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD,BD于点M,P,CD交BE于点Q,连接PQ,BM,下面结论:
①△ABE≌△DBC;②∠DMA=60°;③△BPQ为等边三角形;④MB平分∠AMC,
其中结论正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形ABCD各顶点的坐标分别为A(0,1)、B(5,1)、C(7,3)、D(2,5).
(1)填空:四边形ABCD内(边界点除外)一共有 个整点(即横坐标和纵坐标都是整数的点);
(2)求四边形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
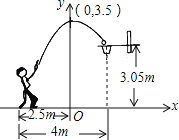
【题目】一位篮球运动员在距离篮圈中心水平距离4m处起跳投篮,球沿一条抛物线运动,当球运动的水平距离为2.5m时,达到最大高度3.5m,然后准确落入篮框内.已知篮圈中心距离地面高度为3.05m,在如图所示的平面直角坐标系中,下列说法正确的是( )
A. 此抛物线的解析式是y=﹣![]() x2+3.5
x2+3.5
B. 篮圈中心的坐标是(4,3.05)
C. 此抛物线的顶点坐标是(3.5,0)
D. 篮球出手时离地面的高度是2m
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com