
����Ŀ���Ķ����ϲ��ѽ����̲���������
���⣺�ڹ���x��y�Ķ�Ԫһ�η�����![]() �У�x>1��y<0����a��ȡֵ��Χ��
�У�x>1��y<0����a��ȡֵ��Χ��
�ڹ���x��y�Ķ�Ԫһ�η������У����ò���a�Ĵ���ʽ��ʾx��y��Ȼ�����x>1��y<0�г����ڲ���a�IJ���ʽ�鼴�����a��ȡֵ��Χ��
�⣺��![]() �����
����� ������Ϊx>1��y<0������
������Ϊx>1��y<0������ �����________��
�����________��
���㰴����������������������⣺
��֪x-y=4��x>3��y<1����x+y��ȡֵ��Χ��

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
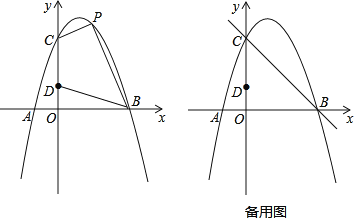
����Ŀ����ͼ���Գ���Ϊֱ��x��1�������߾���A����1��0����C��0��3�����㣬��x�����һ������ΪB����D��y���ϣ���OB��3OD
��1����������ߵı���ʽ��
��2������������ϵ�һ������P�ĺ�����Ϊt
�ٵ�0��t��3ʱ�����ı���CDBP�����S��t�ĺ�����ϵʽ�������S�����ֵ��
�ڵ�Q��ֱ��BC�ϣ�����CDΪ�ߣ���C��D��Q��PΪ������ı�����ƽ���ı��Σ���������з��������ĵ�P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�У���A=��C=90����BE��DF�ֱ��ǡ�ABC����ADC��ƽ���ߣ�

��1����1���2��ʲô��ϵ��Ϊʲô��
��2��BE��DF��ʲô��ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���֪AB=BC=CA=4cm��AD��BC��D����P��Q�ֱ��B��C����ͬʱ���������е�P��BC���յ�C�˶����ٶ�Ϊ1cm/s����Q��CA��AB���յ�B�˶����ٶ�Ϊ2cm/s���������˶���ʱ��Ϊx��s����
��1����xΪ��ֵʱ��PQ��AC��
��2�����PQD�����Ϊy��cm2������0��x��2ʱ����y��x�ĺ�����ϵʽ��
��3����0��x��2ʱ����֤��ADƽ�֡�PQD�������
��4��̽����PQΪֱ����Բ��AC��λ�ù�ϵ����д����Ӧλ�ù�ϵ��x��ȡֵ��Χ����Ҫ��д�����̣���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�������������A��B��C��������������������¶��壺��ˮƽ����a��������������������ֵ����Ǧ������h���������������������ֵ�������������S=ah�����磬��������ֱ�ΪA��0��3����B��-3��4����C��1��-2��������ˮƽ����a=4����Ǧ������h=6�����������S=ah=24����D��2��2����E��-2��-1����F��3��m����������������Ϊ20����m��ֵΪ______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ��
��![]() ��ֱ����
��ֱ����![]() ��
��
��1����֤��![]() ��
��![]() �����ߣ�
�����ߣ�
��2������![]() ��
��![]() ���е㣬����
���е㣬����![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ��
��![]() ʱ����
ʱ����![]() ��ֵ��
��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���A��B��C������ֱ�ΪA��a��3����B��b��6����C��m+6��1������a��b����![]()

��1�����ú�m��ʽ�ӱ�ʾA��B��������ꣻ
��2����ͼ����A�ڵڶ����ޣ���B�ڵ�һ���ޣ�����A��B��C��O�ĵ㣻
������B��y��ľ��벻С�ڵ�A��y������2��������m��ȡֵ��Χ��
����������AOC���������������ABC�����![]() ����ʵ��m��ֵ��
����ʵ��m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��MN��PQ��ֱ��AB�ֱ���MN��PQ�ཻ�ڵ�A��B��С��ͬѧ���ó߹水���²�����ͼ�����Ե�AΪԲ�ģ������ⳤΪ�뾶������AN�ڵ�C����AB�ڵ�D�����ֱ���C��DΪԲ�ģ��Դ���![]() CD��Ϊ�뾶��������������NAB�ڽ��ڵ�E����������AE��PQ�ڵ�F����AB=2����ABP=60�������߶�AF�ij�Ϊ_____��
CD��Ϊ�뾶��������������NAB�ڽ��ڵ�E����������AE��PQ�ڵ�F����AB=2����ABP=60�������߶�AF�ij�Ϊ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC�У���BΪԲ�ģ�BC��Ϊ�뾶�������ֱ�AC��AB��D��E���㣬������BD��DE������A=30�㣬AB=AC������BDE=______��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com