
【题目】在平面直角坐标系中,点A,B,C的坐标分别为A(a,3),B(b,6),C(m+6,1),且a,b满足![]()

(1)请用含m的式子表示A,B两点的坐标;
(2)如图,点A在第二象限,点B在第一象限,连接A、B、C、O四点;
①若点B到y轴的距离不小于点A到y轴距离的2倍,试求m的取值范围;
②若三角形AOC的面积等于三角形ABC面积的![]() ,求实数m的值.
,求实数m的值.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)解二元一次方程组求出a,b的值,即可用含m的式子表示A,B两点的坐标;
(2)①根据点的坐标性质、结合题意列出不等式,计算即可;
②分别求出△ABC的面积和△AOC的面积,根据题意列方程,解方程得到答案.
(1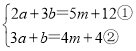 ,
,
②×3-①得,7a=7m,
解得,a=m,
把a=m代入①得,b=m+4,
则A点的坐标为(m,3),B点的坐标为(m+4,6);
(2)①∵点A在第二象限,点B在第一象限,
∴m<0,m+4>0,
解得,-4<m<0,
由题意得,m+4≥-2m,
解得,m≥-![]() ,
,
则-![]() ≤m<0;
≤m<0;
②△AOC的面积=![]() ×(1+3)×(m+6-m)-
×(1+3)×(m+6-m)-![]() ×(-m)×3-
×(-m)×3-![]() ×(m+6)×1=m+9,
×(m+6)×1=m+9,
△ABC的面积=![]() ×(3+5)×(m+6-m)-
×(3+5)×(m+6-m)-![]() ×(m+4-m)×3-
×(m+4-m)×3-![]() ×(m+6-m-4)×5=13,
×(m+6-m-4)×5=13,
由题意得,m+9=![]() ×13,
×13,
解得,m=-![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点![]() ,试分别根据下列条件,求出点
,试分别根据下列条件,求出点![]() 的坐标。
的坐标。
(1)点![]() 在
在![]() 轴上;
轴上;
(2)点![]() 横坐标比纵坐标大3;
横坐标比纵坐标大3;
(3)点![]() 在过
在过![]() 点,且与
点,且与![]() 轴平行的直线上。
轴平行的直线上。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰直角三角形ABC,AB=AC,∠BAC=∠BDC=90°,

(1)若∠DBA=20°,则∠ACD=______°;
(2)连接AD,则∠ADB=______°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料并把解答过程补充完整.
问题:在关于x,y的二元一次方程组![]() 中,x>1,y<0,求a的取值范围.
中,x>1,y<0,求a的取值范围.
在关于x,y的二元一次方程组中,利用参数a的代数式表示x,y,然后根据x>1,y<0列出关于参数a的不等式组即可求得a的取值范围.
解:由![]() ,解得
,解得 ,又因为x>1,y<0,所以
,又因为x>1,y<0,所以 ,解得________.
,解得________.
请你按照上述方法,完成下列问题:
已知x-y=4,x>3,y<1,求x+y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D、E、F分别在BC、AB、AC边上,且BE=CF, BD=CE.

(1)求证:△DEF是等腰三角形;
(2)当∠A=40°时,求∠DEF的度数;
(3)△DEF可能是等腰直角三角形吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B、C在数轴上分别表示的数为-10,2,8,点D是BC中点,点E是AD中点.
(1)求EB的长;
(2)若动点P从点A出发,以1cm/s的速度向点C运动,达到点C停止运动,点Q从点C出发,以2cm/s的速度向点A运动,到达点A停止运动,若运动时间为ts,当t为何值时,PQ=3cm?
(3)点A,B,C开始在数轴上运动,若点A以1cm/s的速度向左运动,同时,点B和点C分别以4cm/s和9cm/s的速度向右运动,假设t秒钟过后,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB,请问:AB-BC的值是否随时间t的变化而变化?若变化,请说明理由;若不变,请求其常数值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是我们生活中经常接触的小刀,刀片的外壳是四边形,而且刀片外壳与刀片铆合部分都是直角,刀片的上、下是平行的,转动刀片时会形成∠1和∠2,则∠1+∠2的度数为( )

A. 80° B. 70° C. 90° D. 100°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,AD是△ABC的中线.△ABD与△ACD的面积有怎样的数量关系?为什么?

(2)若三角形的面积记为S,例如:△ABC的面积记为S△ABC.如图②,已知S△ABC=1.△ABC的中线AD、CE相交于点O,求四边形BDOE的面积.

小华利用(1)的结论,解决了上述问题,解法如下:
连接BO,设S△BEO=x,S△BDO=y,由(1)结论可得:S△BCE=S△BAD=![]() S△ABC=
S△ABC=![]() ,S△BCO=2S△BDO=2y,S△BAO=2S△BEO=2x.则有
,S△BCO=2S△BDO=2y,S△BAO=2S△BEO=2x.则有 即
即 所以x+y=
所以x+y=![]() .即四边形BDOE面积为
.即四边形BDOE面积为![]() .
.
请仿照上面的方法,解决下列问题:
①如图③,已知S△ABC=1.D、E是BC边上的三等分点,F、G是AB边上的三等分点,AD、CF交于点O,求四边形BDOF的面积.

②如图④,已知S△ABC=1.D、E、F是BC边上的四等分点,G、H、I是AB边上的四等分点,AD、CG交于点O,则四边形BDOG的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C在一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD,BD于点M,P,CD交BE于点Q,连接PQ,BM,下面结论:
①△ABE≌△DBC;②∠DMA=60°;③△BPQ为等边三角形;④MB平分∠AMC,
其中结论正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com