
【题目】等腰直角三角形ABC,AB=AC,∠BAC=∠BDC=90°,

(1)若∠DBA=20°,则∠ACD=______°;
(2)连接AD,则∠ADB=______°.
【答案】20; 45
【解析】
(1)利用三角形内角和定理求出∠AGB,根据对顶角相等求出∠CGD即可解决问题;
(2)由说明△CGD∽△BGA,得到![]() ,进而得到△CGB∽△DGA,可得∠ADG=∠BCG解决问题;
,进而得到△CGB∽△DGA,可得∠ADG=∠BCG解决问题;
解:(1)
∵∠DBA=20°,∠BAG=90°,
∴∠BGA=90°-20°=70°,
∴∠CGD=∠AGB=70°,
∵∠CDG=90°,
∴∠DCG=90°-70°=20°,
故答案为20.
(2)∵∠CGD=∠BGA,∠CDG=∠BAG=90°,
∴△CGD∽△BGA,
∴![]() =
=![]() ,
,
∵∠CGB=∠DGA,
∴△CGB∽△DGA,
∴∠ADG=∠BCG,
∵AB=AC,∠BAC=90°,
∴∠ACB=45°,
∴∠ADB=∠BCG=45°,
故答案为45.


科目:初中数学 来源: 题型:
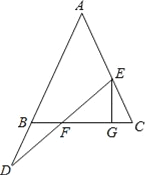
【题目】如图,在△ABC中,AB=AC,点E在线段AC上,D在AB的延长线上,连接DE交BC于F,过E作EG⊥BC于G.
(1)下列两个关系式:①DB=EC,②DF=EF,请你选择一个做为条件,另一个做为结论构成一个正确的命题,并给予证明.
你选择的条件是 ,结论是 .(只需填序号)
(2)在(1)的条件下,求证:FG=BC/2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市在2013年义务教育质量监测过程中,为了解学生的家庭教育情况,就八年级学生平时主要和谁在一起生活进行了抽样调查.下面是根据这次调查情况制作的不完整的频数分布表和扇形统计图.

频数分布表
代码 | 和谁一起生活 | 频数 | 频率 |
A | 父母 | 4200 | 0.7 |
B | 爷爷奶奶 | 660 | a |
C | 外公外婆 | 600 | 0.1 |
D | 其它 | b | 0.09 |
合计 | 6000 | 1 |
请根据上述信息,回答下列问题:
(1)a= ,b= ;
(2)在扇形统计图中,和外公外婆一起生活的学生所对应扇形圆心角的度数是 ;
(3)若该市八年级学生共有3万人,估计不与父母一起生活的学生有 人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠A=∠C=90°,BE,DF分别是∠ABC,∠ADC的平分线.

(1)∠1与∠2有什么关系,为什么?
(2)BE与DF有什么关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于受到手机更新换代的影响,某手机店经销的华为P10 plus手机四月售价比三月每台降价500元.如果卖出相同数量的华为P10 plus手机,那么三月销售额为9万元,四月销售额只有8万元.
(1)三月华为P10 plus手机每台售价为多少元?
(2)为了提高利润,该店计划五月购进华为P20 pro手机销售,已知华为P10 plus每台进价为3500元,华为P20 pro每台进价为4000元,预计用不多于7.6万元且不少于7.4万元的资金购进这两种手机共20台,请问有几种进货方案?
(3)该店计划六月对华为P10 plus的尾货进行销售,决定在四月售价基础上每售出一台华为P10 plus手机再返还顾客现金![]() 元,而华为P20 pro按销售价4400元销售,如要使(2)中所有方案获利相同,
元,而华为P20 pro按销售价4400元销售,如要使(2)中所有方案获利相同,![]() 应取何值?
应取何值?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,已知AB=BC=CA=4cm,AD⊥BC于D,点P、Q分别从B、C两点同时出发,其中点P沿BC向终点C运动,速度为1cm/s;点Q沿CA、AB向终点B运动,速度为2cm/s,设它们运动的时间为x(s).
(1)求x为何值时,PQ⊥AC;
(2)设△PQD的面积为y(cm2),当0<x<2时,求y与x的函数关系式;
(3)当0<x<2时,求证:AD平分△PQD的面积;
(4)探索以PQ为直径的圆与AC的位置关系,请写出相应位置关系的x的取值范围(不要求写出过程).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,对于任意三点A,B,C的“矩面积”,给出如下定义:“水平底”a:任意两点横坐标差的最大值,“铅垂高”h:任意两点纵坐标差的最大值,则“矩面积”S=ah.例如,三点坐标分别为A(0,3),B(-3,4),C(1,-2),则“水平底”a=4,“铅垂高”h=6,“矩面积”S=ah=24.若D(2,2),E(-2,-1),F(3,m)三点的“矩面积”为20,则m的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A,B,C的坐标分别为A(a,3),B(b,6),C(m+6,1),且a,b满足![]()

(1)请用含m的式子表示A,B两点的坐标;
(2)如图,点A在第二象限,点B在第一象限,连接A、B、C、O四点;
①若点B到y轴的距离不小于点A到y轴距离的2倍,试求m的取值范围;
②若三角形AOC的面积等于三角形ABC面积的![]() ,求实数m的值.
,求实数m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图在△ABC中,AD、BE分别是BC,AC边上的高,AD、BE交于H,DA=DB,BH=AC,点F为BH的中点,∠ABE=15°.
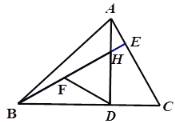
(1)求证:△ADC≌△BDH
(2)求证:DC=DF
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com