
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若点![]() 是
是![]() 的中点,连接
的中点,连接![]() 交
交![]() 于点
于点![]() ,当
,当![]() ,
,![]() 时,求
时,求![]() 的值.
的值.

【答案】(1)见解析;(2)![]()
【解析】
(1)证明△ADC∽△BAC,可得∠BAC=∠ADC=900,从而可判断AC是⊙O的切线;
(2)根据(1)所得△ADC∽△BAC,可得出CA的长度,从而判断∠CFA=∠CAF,利用等腰三角形的性质得出AF的长度,继而得出DF的长,在Rt△AFD中利用勾股定理可得出AF的长.
(1)∵AB是⊙O的直径,
∴∠ADB=∠ADC=90°,
∵∠B=∠CAD,∠C=∠C,
∴△ADC∽△BAC,
∴∠BAC=∠ADC=90°,
∴BA⊥AC,
∴AC是⊙O的切线.
(2)∵BD=5,CD=4,
∴BC=9,
∵△ADC∽△BAC(已证),
∴![]() ,即AC2=BC×CD=36,
,即AC2=BC×CD=36,
解得:AC=6,
在Rt△ACD中,AD= ![]() ,
,
∵∠CAF=∠CAD+∠DAE=∠ABF+∠BAE=∠AFD,
∴CA=CF=6,
∴DF=CA-CD=2,
在Rt△AFD中,AF= ![]() .
.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
【题目】(2017重庆A卷第11题)如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米,则此时AB的长约为( )(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84).
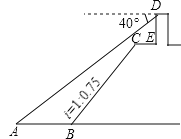
A. 5.1米 B. 6.3米 C. 7.1米 D. 9.2米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABC ∠ACB ,BD 、CD 分别平分△ABC 的内角 ∠ABC 、外角 ∠ACP ,BE平分外角 ∠MBC 交 DC 的延长线于点 E ,以下结论:①∠BDE ![]() ∠BAC ;② DB⊥BE ;③∠BDC ∠ACB 90 ;④∠BAC 2∠BEC 180 .其中正确的结论有( )
∠BAC ;② DB⊥BE ;③∠BDC ∠ACB 90 ;④∠BAC 2∠BEC 180 .其中正确的结论有( )
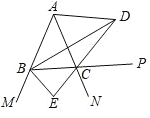
A.1 个B.2 个C.3 个D.4 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知命题“等腰三角形两腰上的高线长相等”
(1)请写出该命题的逆命题;
(2)判断(1)中命题的真假,并画出图形,补充已知,求证,及证明过程.
图形:
已知:在△ABC中,CD⊥AB,BE⊥AC,且______.
求证:______.
证明:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料并把解答过程补充完整.
问题:在关于x,y的二元一次方程组![]() 中,x>1,y<0,求a的取值范围.
中,x>1,y<0,求a的取值范围.
在关于x,y的二元一次方程组中,利用参数a的代数式表示x,y,然后根据x>1,y<0列出关于参数a的不等式组即可求得a的取值范围.
解:由![]() ,解得
,解得 ,又因为x>1,y<0,所以
,又因为x>1,y<0,所以 ,解得________.
,解得________.
请你按照上述方法,完成下列问题:
已知x-y=4,x>3,y<1,求x+y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAC=30°,AM是∠BAC的平分线,过M作ME∥BA交AC于E,作MD⊥BA,垂足为D,ME=10cm,则MD=_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B、C在数轴上分别表示的数为-10,2,8,点D是BC中点,点E是AD中点.
(1)求EB的长;
(2)若动点P从点A出发,以1cm/s的速度向点C运动,达到点C停止运动,点Q从点C出发,以2cm/s的速度向点A运动,到达点A停止运动,若运动时间为ts,当t为何值时,PQ=3cm?
(3)点A,B,C开始在数轴上运动,若点A以1cm/s的速度向左运动,同时,点B和点C分别以4cm/s和9cm/s的速度向右运动,假设t秒钟过后,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB,请问:AB-BC的值是否随时间t的变化而变化?若变化,请说明理由;若不变,请求其常数值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富同学们的课余生活,某学校将举行“亲近大自然”户外活动.现随机抽取了部分学生进行主题为“你最想去的景点是”的问卷调查,要求学生只能从“A(世博园),B(劳动公园),C(月牙岛公园),D(赫图阿拉城)”四个景点中选择一项,根据调查结果,绘制了如下两幅不完整的统计图:

(1)本次共调查了多少名学生?
(2)补全条形统计图;
(3)在扇形统计图中,求B(劳动公园)部分所占的圆心角度数;
(4)若该学校共有3600名学生,试估计该校最想去月牙岛公园的学生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com