
【题目】已知关于x的方程ax+b=0(a≠0)的解为x=-2,点(1,3)是抛物线y=ax2+bx+c(a≠0)上的一个点,则下列四个点中一定在该抛物线上的是( )
A. (2,3) B. (0,3)
C. (-1,3) D. (-3,3)
科目:初中数学 来源: 题型:
【题目】如图1,矩形ABCD中,E是AD的中点,以点E直角顶点的直角三角形EFG的两边EF,EG分别过点B,C,∠F=30°.
(1)求证:BE=CE
(2)将△EFG绕点E按顺时针方向旋转,当旋转到EF与AD重合时停止转动.若EF,EG分别与AB,BC相交于点M,N.(如图2)
①求证:△BEM≌△CEN;
②若AB=2,求△BMN面积的最大值;
③当旋转停止时,点B恰好在FG上(如图3),求sin∠EBG的值.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方体纸盒的表面积为12cm2;

(1)求正方体的棱长;
(2)剪去盖子后,插入一根长为5cm的细木棒,则细木棒露在外面的最短长度是多少?
(3)一只蚂蚁在纸盒的表面由A爬到B,求蚂蚁行走的最短路线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明想利用太阳光测量楼高,他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:如示意图,小明边移动边观察,发现站到点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得小明落在墙上的影子高度CD=1.2m,CE=0.8m,CA=30m(点A、E、C在同一直线上).已知小明的身高EF是1.7m,请你帮小明求出楼高AB(结果精确到0.1m).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC.已知AB=2,DE=1,BD=8,设CD=x.
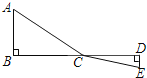
(1)用含x的代数式表示AC+CE的长;
(2)请问点C满足什么条件时,AC+CE的值最小;
(3)根据(2)中的规律和结论,请构图求出代数式![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,AH⊥BC,垂足为H,且AH=6 cm,点D是AB的中点,点P是AH上一动点,则DP与BP和的最小值是__________cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,对于点P(x,y),我们把点P′(﹣y+1,x+1)叫做点P的伴随点.已知点A1的伴随点为A2,点A2的伴随点为A3,点A3的伴随点为A4,…,这样依次得到点A1,A2,A3,…,An,….若点A1的坐标为(a,b),则点A2020的坐标为( )
A.(a,b)B.(﹣b+1,a+1)C.(﹣a,﹣b+2)D.(b﹣1,﹣a+1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com