
【题目】在平面直角坐标系中,对于点P(x,y),我们把点P′(﹣y+1,x+1)叫做点P的伴随点.已知点A1的伴随点为A2,点A2的伴随点为A3,点A3的伴随点为A4,…,这样依次得到点A1,A2,A3,…,An,….若点A1的坐标为(a,b),则点A2020的坐标为( )
A.(a,b)B.(﹣b+1,a+1)C.(﹣a,﹣b+2)D.(b﹣1,﹣a+1)
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知关于x的方程ax+b=0(a≠0)的解为x=-2,点(1,3)是抛物线y=ax2+bx+c(a≠0)上的一个点,则下列四个点中一定在该抛物线上的是( )
A. (2,3) B. (0,3)
C. (-1,3) D. (-3,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.在△AOB中∠AOB=![]() ,OA=OB=10,分别以OA、OB所在直线为坐标轴建立平面直角坐标系(如图所示).点P自点A出发沿线段AB匀速运动到点B停止,同时点D自原点O出发沿x轴正方向匀速运动,在点P、D运动的过程中,始终满足PO=PD,过点O、D向AB作垂线,垂足分别为点C、E,设OD的长为x.
,OA=OB=10,分别以OA、OB所在直线为坐标轴建立平面直角坐标系(如图所示).点P自点A出发沿线段AB匀速运动到点B停止,同时点D自原点O出发沿x轴正方向匀速运动,在点P、D运动的过程中,始终满足PO=PD,过点O、D向AB作垂线,垂足分别为点C、E,设OD的长为x.
(1)求AP的长(用含x的代数式表示)
(2)在点P、D的运动过程中,线段PC与DE是否相等?若相等,请给予证明;若不相等,请说明理由;
(3)设以点P、O、D、E为顶点的四边形的面积为y,请直接写出y与x的函数关系式,并写出自变量的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5)(每个方格的边长均为1个单位长度).
(1)请画出△A1B1C1,使△A1B1C1与△ABC关于x轴对称;
(2)将△ABC绕点O逆时针旋转90°,画出旋转后得到的△A2B2C2,并直接写出点B2,C2的坐标;
(3)若点P(a,b)是△ABC内任意一点,试写出将△ABC绕点O逆时针旋转90°后点P的对应点P2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
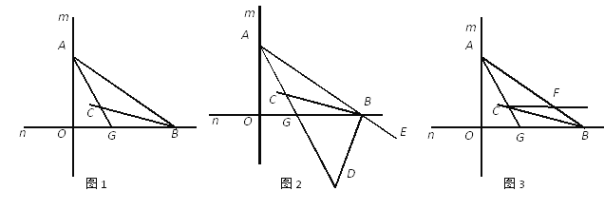
【题目】如图1,直线m与直线n垂直相交于O,点A在直线m上运动,点B 在直线n上运动,AC、BC分别是∠BAO和∠ABO的角平分线.
(1)求∠ACB的大小;
(2)如图2,若BD是△AOB的外角∠OBE的角平分线,BD与AC相交于点D,点A、B在运动的过程中,∠ADB的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出其值;
(3)如图3,过C作直线与AB交于F,且满足∠AGO-∠BCF=45°,求证:CF∥OB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以△ABC的边AB,AC所在直线为对称轴作△ABC的对称图形△ABD和△ACE,∠BAC=150°,线段BD与CE相交于点O,连接BE、ED、DC、OA.有如下结论:①∠EAD=90°;②∠BOE=60°;③OA平分∠BOC;④2EA=ED;⑤BP=EQ.其中正确的结论个数为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,![]() ,
,![]() ,
,![]() ,CP、CM分别是AB上的高和中线,如果圆A是以点A为圆心,半径长为2的圆,那么下列判断正确的是( )
,CP、CM分别是AB上的高和中线,如果圆A是以点A为圆心,半径长为2的圆,那么下列判断正确的是( )
A. 点P,M均在圆A内 B. 点P、M均在圆A外
C. 点P在圆A内,点M在圆A外 D. 点P在圆A外,点M在圆A内
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(a,1),B(b,﹣2),C(0,c),且(a﹣2)2+![]() +|c+2|=0.
+|c+2|=0.
(1)如图1,求A、B、C三点的坐标.
(2)如图2,延长AC至P(﹣a,﹣5),连PO、PB.求![]() .
.
(3)将线段AC平移,使点A的对应点E恰好落在y轴正半轴上,点C的对应点为F,连AF交y轴于G,当EG=3OG时,求点E的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】黄河,既是一条源远流长、波澜壮阔的自然河,又是一条孕育中华民族灿烂文明的母亲河.数学课外实践活动中,小林和同学们在黄河南岸小路上的A,B两点处,用测角仪分别对北岸的观景亭D进行测量.如图,测得∠DAC=45°,∠DBC=65°.若AB=200米,求观景亭D到小路AC的距离约为多少米?(结果精确到1米,参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14)


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com