
【题目】.在△AOB中∠AOB=![]() ,OA=OB=10,分别以OA、OB所在直线为坐标轴建立平面直角坐标系(如图所示).点P自点A出发沿线段AB匀速运动到点B停止,同时点D自原点O出发沿x轴正方向匀速运动,在点P、D运动的过程中,始终满足PO=PD,过点O、D向AB作垂线,垂足分别为点C、E,设OD的长为x.
,OA=OB=10,分别以OA、OB所在直线为坐标轴建立平面直角坐标系(如图所示).点P自点A出发沿线段AB匀速运动到点B停止,同时点D自原点O出发沿x轴正方向匀速运动,在点P、D运动的过程中,始终满足PO=PD,过点O、D向AB作垂线,垂足分别为点C、E,设OD的长为x.
(1)求AP的长(用含x的代数式表示)
(2)在点P、D的运动过程中,线段PC与DE是否相等?若相等,请给予证明;若不相等,请说明理由;
(3)设以点P、O、D、E为顶点的四边形的面积为y,请直接写出y与x的函数关系式,并写出自变量的取值范围.

【答案】见解析.
【解析】
(1)作PG⊥x轴于点G,PF⊥y轴于点F,在Rt△APF中,∠PAF=45°,PF=APsin45°=![]() AP,
AP,![]() =
=![]() AP,所以AP=
AP,所以AP=![]() x;
x;
(2)分两种情况①当0≤x<10时;②当10≤x≤20时;
(3)①当0<x<10时,S四边形PODE=S△AOB-S△AOP-S△DEB;②当10≤x≤20时, S四边形PODE=S△POD+S△DOE.
解:(1)作PG⊥x轴于点G,PF⊥y轴于点F,
在Rt△APF中,∠PAF=45°,PF=APsin45°=![]() AP,
AP,
∵OG=PF,即![]() =
=![]() AP,
AP,
∴AP=![]() x ;
x ;

(2)结论:PC=BE.
①当0≤x<10时,
∵PC=AC-AP=5![]() -
-![]() x,BE=
x,BE=![]() BD=
BD=![]() (10-x)═
(10-x)═![]() ,
,
∴PC=BE,
②当10≤x≤20时,如图

∵PC=AP-AC=![]() ,BE=
,BE=![]() BD=
BD=![]() (x-10)=
(x-10)=![]() ,
,
∴PC=BE,
综合①②PC=BE;
(3)①当0<x<10时,
S四边形PODE=S△AOB-S△AOP-S△DEB=![]()
![]() =-
=-![]() x2+
x2+![]() x+25,
x+25,
②当10≤x≤20时,
S四边形PODE=S△POD+S△DOE=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知正方体纸盒的表面积为12cm2;

(1)求正方体的棱长;
(2)剪去盖子后,插入一根长为5cm的细木棒,则细木棒露在外面的最短长度是多少?
(3)一只蚂蚁在纸盒的表面由A爬到B,求蚂蚁行走的最短路线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,AH⊥BC,垂足为H,且AH=6 cm,点D是AB的中点,点P是AH上一动点,则DP与BP和的最小值是__________cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式,例如图1可以得到![]() ,请解答下列问题:
,请解答下列问题:

(1)图2所表示的数学等式为_____________________;
(2)利用(1)得到的结论,解决问题: 若![]() ,求
,求![]() 的值;
的值;
(3)如图3,将两个边长分别为a和b的正方形拼在一起,![]() 三点在同一直线上,连接
三点在同一直线上,连接![]() ,若两正方形的边长满足
,若两正方形的边长满足![]()
![]() 求阴影部分面积.
求阴影部分面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是BC的中点,AB⊥BC,DC⊥BC,AE平分∠BAD,下列结论:①∠AED=90°②∠ADE=∠CDE③DE=BE④AD=AB+CD,四个结论中成立的是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
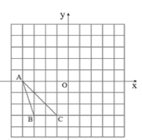
【题目】如图,在边长为1的正方形网格中,△ABC的顶点均在格点上.
(1)画出△ABC关于原点成中心对称的△A′B′C′,并直接写出△A′B′C′各顶点的坐标;
(2)连接BC′,B′C,求四边形BCB′C′的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,对于点P(x,y),我们把点P′(﹣y+1,x+1)叫做点P的伴随点.已知点A1的伴随点为A2,点A2的伴随点为A3,点A3的伴随点为A4,…,这样依次得到点A1,A2,A3,…,An,….若点A1的坐标为(a,b),则点A2020的坐标为( )
A.(a,b)B.(﹣b+1,a+1)C.(﹣a,﹣b+2)D.(b﹣1,﹣a+1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请把下面证明过程补充完整
如图,已知AD⊥BC于D,点E在BA的延长线上,EG⊥BC于C,交AC于点F,∠E=∠1.求证:AD平分∠BAC.

证明:∵AD⊥BC于D,EG⊥BC于G( ),
∴∠ADC=∠EGC=90°( ),
∴AD∥EG( ),
∴∠1=∠2( ),
∴_____=∠3( ),
又∵∠E=∠1(已知),∴∠2=∠3( ),
∴AD平分∠BAC( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com