
【题目】请把下面证明过程补充完整
如图,已知AD⊥BC于D,点E在BA的延长线上,EG⊥BC于C,交AC于点F,∠E=∠1.求证:AD平分∠BAC.

证明:∵AD⊥BC于D,EG⊥BC于G( ),
∴∠ADC=∠EGC=90°( ),
∴AD∥EG( ),
∴∠1=∠2( ),
∴_____=∠3( ),
又∵∠E=∠1(已知),∴∠2=∠3( ),
∴AD平分∠BAC( )
【答案】已知;垂直的定义;同位角相等,两直线平行;两直线平行,内错角相等;∠E;两直线平行,同位角相等;等量代换;角平分线的定义.
【解析】
已知垂直AD⊥BC于D,EG⊥BC于G,可推得∠ADC=∠EGC=90°,同位角相等可推出两条直线平行,两条直线平行可推得,内错角和同位角相等,再利用等量代换,可得AD平分∠BAC.
∵AD⊥BC于D,EG⊥BC于G(已知),
∴∠ADC=∠EGC=90°( 垂直的定义),
∴AD∥EG( 同位角相等,两直线平行),
∴∠1=∠2( 两直线平行,内错角相等),
∴∠E=∠3( 两直线平行,同位角相等),
又∵∠E=∠1(已知),
∴∠2=∠3( 等量代换),
∴AD平分∠BAC( 角平分线的定义).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】.在△AOB中∠AOB=![]() ,OA=OB=10,分别以OA、OB所在直线为坐标轴建立平面直角坐标系(如图所示).点P自点A出发沿线段AB匀速运动到点B停止,同时点D自原点O出发沿x轴正方向匀速运动,在点P、D运动的过程中,始终满足PO=PD,过点O、D向AB作垂线,垂足分别为点C、E,设OD的长为x.
,OA=OB=10,分别以OA、OB所在直线为坐标轴建立平面直角坐标系(如图所示).点P自点A出发沿线段AB匀速运动到点B停止,同时点D自原点O出发沿x轴正方向匀速运动,在点P、D运动的过程中,始终满足PO=PD,过点O、D向AB作垂线,垂足分别为点C、E,设OD的长为x.
(1)求AP的长(用含x的代数式表示)
(2)在点P、D的运动过程中,线段PC与DE是否相等?若相等,请给予证明;若不相等,请说明理由;
(3)设以点P、O、D、E为顶点的四边形的面积为y,请直接写出y与x的函数关系式,并写出自变量的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,![]() ,
,![]() ,
,![]() ,CP、CM分别是AB上的高和中线,如果圆A是以点A为圆心,半径长为2的圆,那么下列判断正确的是( )
,CP、CM分别是AB上的高和中线,如果圆A是以点A为圆心,半径长为2的圆,那么下列判断正确的是( )
A. 点P,M均在圆A内 B. 点P、M均在圆A外
C. 点P在圆A内,点M在圆A外 D. 点P在圆A外,点M在圆A内
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(a,1),B(b,﹣2),C(0,c),且(a﹣2)2+![]() +|c+2|=0.
+|c+2|=0.
(1)如图1,求A、B、C三点的坐标.
(2)如图2,延长AC至P(﹣a,﹣5),连PO、PB.求![]() .
.
(3)将线段AC平移,使点A的对应点E恰好落在y轴正半轴上,点C的对应点为F,连AF交y轴于G,当EG=3OG时,求点E的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,由相同边长的小正方形组成的网格图形,A、B、C都在格点上,利用网格画图:(注:所画线条用黑色签字笔描黑)
(1)过点C画AB的平行线CF,标出F点;
(2)过点B画AC的垂线BG,垂足为点G,标出G点;
(3)点B到AC的距离是线段 的长度;
(4)线段BG、AB的大小关系为:BG AB(填“>”、“<”或“=”),理由是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
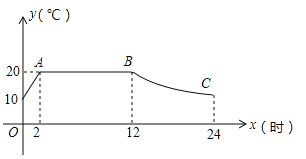
【题目】我市某蔬菜生产基地用装有恒温系统的大棚栽培一种适宜生长温度为15﹣20℃的新品种,如图是某天恒温系统从开启到关闭及关闭后,大棚里温度y(℃)随时间x(h)变化的函数图象,其中AB段是恒温阶段,BC段是双曲线![]() 的一部分,请根据图中信息解答下列问题:
的一部分,请根据图中信息解答下列问题:
(1)求k的值;
(2)恒温系统在一天内保持大棚里温度在15℃及15℃以上的时间有多少小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
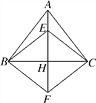
【题目】如图,在等腰三角形ABC中,AB=AC,AH⊥BC,点E是AH上一点,延长AH至点F,使FH=EH.
(1)求证:四边形EBFC是菱形;
(2)如果∠BAC=∠ECF,求证:AC⊥CF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】黄河,既是一条源远流长、波澜壮阔的自然河,又是一条孕育中华民族灿烂文明的母亲河.数学课外实践活动中,小林和同学们在黄河南岸小路上的A,B两点处,用测角仪分别对北岸的观景亭D进行测量.如图,测得∠DAC=45°,∠DBC=65°.若AB=200米,求观景亭D到小路AC的距离约为多少米?(结果精确到1米,参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14)


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com