
【题目】如图,在平面直角坐标系xOy中,矩形AOCD的顶点A的坐标是(0,4),现有两动点P,Q,点P从点O出发沿线段OC(不包括端点O,C)以每秒2个单位长度的速度匀速向点C运动,点Q从点C出发沿线段CD(不包括端点C,D)以每秒1个单位长度的速度匀速向点D运动.点P,Q同时出发,同时停止,设运动时间为t(秒),当t=2(秒)时,PQ=2 ![]() .
. 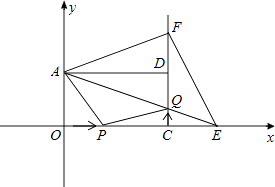
(1)求点D的坐标,并直接写出t的取值范围.
(2)连接AQ并延长交x轴于点E,把AE沿AD翻折交CD延长线于点F,连接EF,则△AEF的面积S是否随t的变化而变化?若变化,求出S与t的函数关系式;若不变化,求出S的值.
(3)在(2)的条件下,t为何值时,四边形APQF是梯形?
【答案】
(1)解:由题意可知,当t=2(秒)时,OP=4,CQ=2,
在Rt△PCQ中,由勾股定理得:PC= ![]() =4,
=4,
∴OC=OP+PC=4+4=8,
又∵矩形AOCD,A(0,4),∴D(8,4).
点P到达终点所需时间为 ![]() =4秒,点Q到达终点所需时间为
=4秒,点Q到达终点所需时间为 ![]() =4秒,由题意可知,t的取值范围为:0<t<4.
=4秒,由题意可知,t的取值范围为:0<t<4.
(2)解:结论:△AEF的面积S不变化.
∵AOCD是矩形,∴AD∥OE,∴△AQD∽△EQC,
∴ ![]() ,即
,即 ![]() ,解得CE=
,解得CE= ![]() .
.
由翻折变换的性质可知:DF=DQ=4﹣t,则CF=CD+DF=8﹣t.
S=S梯形AOCF+S△FCE﹣S△AOE
= ![]() (OA+CF)OC+
(OA+CF)OC+ ![]() CFCE﹣
CFCE﹣ ![]() OAOE
OAOE
= ![]() [4+(8﹣t)]×8+
[4+(8﹣t)]×8+ ![]() (8﹣t)
(8﹣t) ![]() ﹣
﹣ ![]() ×4×(8+
×4×(8+ ![]() )
)
化简得:S=32为定值.
所以△AEF的面积S不变化,S=32.
(3)解:若四边形APQF是梯形,因为AP与CF不平行,所以只有PQ∥AF.
由PQ∥AF可得:△CPQ∽△DAF,
∴ ![]() ,即
,即 ![]() ,化简得t2﹣12t+16=0,
,化简得t2﹣12t+16=0,
解得:t1=6+2 ![]() ,t2=6﹣2
,t2=6﹣2 ![]() ,
,
由(1)可知,0<t<4,∴t1=6+2 ![]() 不符合题意,舍去.
不符合题意,舍去.
∴当t=(6﹣2 ![]() )秒时,四边形APQF是梯形.
)秒时,四边形APQF是梯形.
【解析】(1)利用勾股定理求出PC的长度,然后利用矩形的性质确定D点的坐标;自变量的取值范围由动点到达终点的时间来确定;(2)本问关键是利用相似三角形与翻折变换的性质,求出S的表达式.注意求图形面积的方法S=S梯形AOCF+S△FCE﹣S△AOE . 经化简计算后,S=32为定值,所以S不变;(3)由四边形APQF是梯形,可得PQ∥AF,从而得到相似三角形△CPQ∽△DAF;再由线段比例关系求出时间t.
【考点精析】关于本题考查的梯形的定义和翻折变换(折叠问题),需要了解一组对边平行,另一组对边不平行的四边形是梯形.两腰相等的梯形是等腰梯形;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,AC=BC,∠ACB=90°,点D为边AB上一点,CD绕点D顺时针旋转90°至DE,CE交AB于点G.已知AD=8,BG=6,点F是AE的中点,连接DF,求线段DF的长 . 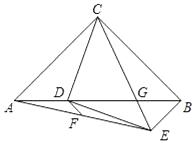
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,AB:BC=3:4,AC=5,点P从点A出发,以每秒1个单位的速度,沿△ABC边A→B→C→A的方向运动,运动时间为t秒.
(1)求AB与BC的长;
(2)在点P的运动过程中,是否存在这样的点P,使△CDP为等腰三角形?若存在,求出t值;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一工地计划租用甲、乙两辆车清理淤泥,从运输量来估算:若租两辆车合运,10天可以完成任务;若单独租用乙车完成任务则比单独租用甲车完成任务多用15天.
(1)甲、乙两车单独完成任务分别需要多少天?
(2)已知两车合运共需租金65000元,甲车每天的租金比乙车每天的租金多1500元.试问:租甲乙车两车、单独租甲车、单独租乙车这三种方案中,哪一种租金最少?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图所示,B、C、D三点在同一条直线上,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )

A. ∠A与∠D互为余角 B. ∠A=∠2 C. △ABC≌△ CED D. ∠1=∠2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABE,△BCD均为等边三角形,点A,B,C在同一条直线上,连接AD,EC,AD与EB相交于点M,BD与EC相交于点N,下列说法正确的有:___________
①AD=EC;②BM=BN;③MN∥AC;④EM=MB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD绕点A逆时针旋转30°,得到平行四边形AB′C′D′,点B′恰好落在BC边土,B′C′和CD交于点P,则∠B′PD的度数是( )

A. 105° B. 120° C. 130° D. 135°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】求代数式的值.
(1)(6a2﹣2ab)﹣2(3a2+4ab﹣![]() b2)其中a=
b2)其中a=![]() ,b=﹣1.
,b=﹣1.
(2)已知A=a2﹣2ab+b2,B=a2+2ab+b2
①求2A﹣B;
②如果2A﹣3B+C=0,那么C的表达式是什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com