
【题目】如图,在矩形ABCD中,CD=2,以点C为圆心,CD长为半径画弧,交AB边于点E,且E为AB中点,则图中阴影部分的面积为 . 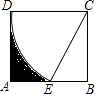
科目:初中数学 来源: 题型:
【题目】为了解我市某中学九年级学生的体能情况,在该校800名九年级学生中随机抽取了部分学生进行引体向上测试,现对这部分学生引体向上的次数进行统计,并绘制成如图所示的频数分布直方图.
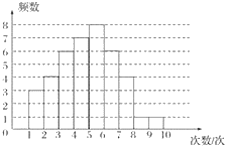
(1)求共抽取了多少名学生进行引体向上测试?
(2)试估计该校九年级学生引体向上次数不低于5次的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
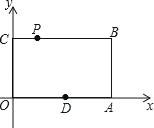
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(6,0)、(0,4),点P是线段BC上的动点,当△OPA是等腰三角形时,则P点的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题情境】
如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.

【探究展示】
(1)证明:AM=AD+MC;
(2)AM=DE+BM是否成立?若成立,请给出证明;若不成立,请说明理由.
【拓展延伸】
(3)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,探究展示(1)、(2)中的结论是否成立?请分别作出判断,不需要证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的边长为2,∠A=60°,一个以点B为顶点的60°角绕点B旋转,这个角的两边分别与线段AD的延长线及CD的延长线交于点P、Q,设DP=x,DQ=y,则能大致反映y与x的函数关系的图象是( )
A.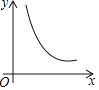
B.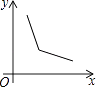
C.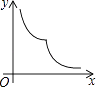
D.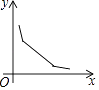
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装厂生产一批男衬衫,经过抽样调查60名中年男子,得知所需衬衫型号的人数如表所示.求出它的中位数是74,众数是76,平均数是74.6,下列说法正确的是( )

A. 所需78号人数太少,78号的可以不生产
B. 这批衬衫可以一律按身长是74.6这个平均数生产
C. 因为众数是76,故76号的生产量要占第一位
D. 因为中位数是74,故74号的生产量要占第一位
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:![]() ,
,![]() ,
,![]() ,则以上三个等式两边分别相加得:
,则以上三个等式两边分别相加得:![]() .
.
![]() 观察发现
观察发现
![]() ______;
______;![]() ______.
______.
![]() 拓展应用
拓展应用
有一个圆,第一次用一条直径将圆周分成两个半圆![]() 如图
如图![]() ,在每个分点标上质数m,记2个数的和为
,在每个分点标上质数m,记2个数的和为![]() ;第二次再将两个半圆周都分成
;第二次再将两个半圆周都分成![]() 圆周
圆周![]() 如图
如图![]() ,在新产生的分点标上相邻的已标的两数之和的
,在新产生的分点标上相邻的已标的两数之和的![]() ,记4个数的和为
,记4个数的和为![]() ;第三次将四个
;第三次将四个![]() 圆周分成
圆周分成![]() 圆周
圆周![]() 如图
如图![]() ,在新产生的分点标上相邻的已标的两数之和的
,在新产生的分点标上相邻的已标的两数之和的![]() ,记8个数的和为
,记8个数的和为![]() ;第四次将八个
;第四次将八个![]() 圆周分成
圆周分成![]() 圆周,在新产生的分点标上相邻的已标的两个数的和的
圆周,在新产生的分点标上相邻的已标的两个数的和的![]() ,记16个数的和为
,记16个数的和为![]() ;
;![]() 如此进行了n次.
如此进行了n次.
![]() ______
______![]() 用含m、n的代数式表示
用含m、n的代数式表示![]() ;
;
![]() 当
当![]() 时,求
时,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国淡水资源短缺问题十分突出,已成为我国经济和社会可持续发展的重要制约因素,节约用水是各地的一件大事.某校初三学生为了调查居民用水情况,随机抽查了某小区20户家庭的月用水量,结果如表所示:

(1)求这20户家庭月用水量的平均数、众数及中位数.
(2)政府为了鼓励节约用水,拟试行水价浮动政策.即设定每个家庭月基本用水量a(t),家庭月用水量不超过a(t)的部分按原价收费,超过a(t)的部分加倍收费.
①你认为以平均数作为该小区的家庭月基本用水量a(t)合理吗?为什么?(简述理由)
②你认为该小区的家庭月基本用水量a(t)为多少时较为合理?为什么?(简述理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某社区超市第一次用6000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的![]() 倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
甲 | 乙 | |
进价(元/件) | 22 | 30 |
售价(元/件) | 29 | 40 |
(1)该超市购进甲、乙两种商品各多少件?
(2)该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(3)该超市第二次以第一次的进价又购进甲、乙两种商品,其中甲商品的件数不变,乙商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多180元,求第二次乙商品是按原价打几折销售?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com