Question

如果一次函数y=-x+1的图象与x轴、y轴分别交于点A点、B点，点M在x轴上，并且使以点A、B、M为顶点的三角形是等腰三角形，那么这样的点M有

1. A.
   3个
2. B.
   4个
3. C.
   5个
4. D.
   7个

Answer 1

B
分析：分别令一次函数y=-x+1中x=0和y=0求出相应的y与x的值，得到A和B的坐标，进而得到OA与OB的长，利用勾股定理求出AB的长，根据题意可分4种情况考虑，当BM=BA时，由BO垂直于MA，根据三线合一得到O为MA的中点，由OA得长得到OM的长，根据M为x轴负半轴的点写出此时M的坐标即可；当AB=AM时，由AB的长，得到AM的长，进而由AM-OA得到OM的长，写出M的坐标即可；当MA=MB时，此时M与原点O重合，写出M的坐标；当AB=AM时，由AB的长得到AM的长，由OA+AM得到OM的长，写出M的坐标即可．
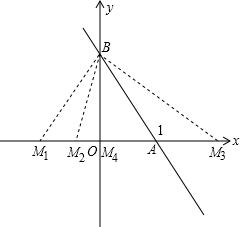
解答：解：一次函数y=-x+1中令x=0，解得y=1；令y=0，解得x=1，
∴A（1，0），B（0，1），即OA=OB=1，
在直角三角形AOB中，根据勾股定理得：AB=，
分四种情况考虑，如图所示：
当BM₁=BA时，由BO⊥AM₁，根据三线合一得到O为M₁A的中点，此时M₁（-1，0）；
当AB=AM₂时，由AB=，得到OM₂=AM₂-OA=-1，此时M₂（1-，0）；
当BA=AM₃时，由AB=，得到AM₃=，则OM₃=OA+AM₃=1+，此时M₃（1+，0）；
当M₄A=M₄B时，此时M₄与原点重合，此时M₄（0，0）．
综上，这样的M点有4个．
故选B．
点评：此题考查了等腰三角形的性质，勾股定理，以及一次函数与坐标轴的交点，利用了数形结合及分类讨论的思想，在分类讨论分情况解决数学问题时，必须认真审题，全面考虑，做到不重不漏，一次分类必须按同标准进行，分出的每一部分不需都是相互独立的．本题要求学生求出相应线段后，注意根据点在坐标轴上的位置选择合适的符号，进而写出坐标．