
【题目】如图,在矩形ABCD中,AB=3,BC=4,将矩形ABCD绕点C按顺时针方向旋转α角,得到矩形A'B'C'D',B'C与AD交于点E,AD的延长线与A'D'交于点F.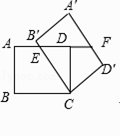
(1)如图①,当α=60°时,连接DD',求DD'和A'F的长;
(2)如图②,当矩形A'B'CD'的顶点A'落在CD的延长线上时,求EF的长;
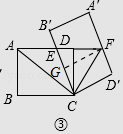
(3)如图③,当AE=EF时,连接AC,CF,求ACCF的值.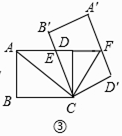
【答案】
(1)
解:①如图①中,∵矩形ABCD绕点C按顺时针方向旋转α角,得到矩形A'B'C'D',
∴A′D′=AD=B′C=BC=4,CD′=CD=A′B′=AB=3∠A′D′C=∠ADC=90°,
∵α=60°,
∴∠DCD′=60°,
∴△CDD′是等边三角形,
∴DD′=CD=3.
②如图①中,连接CF.
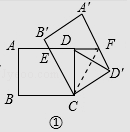
∵CD=CD′,CF=CF,∠CDF=∠CD′F=90°,
∴△CDF≌△CD′F,
∴∠DCF=∠D′CF= ![]() ∠DCD′=30°,
∠DCD′=30°,
在Rt△CD′F中,∵tan∠D′CF= ![]() ,
,
∴D′F= ![]() ,
,
∴A′F=A′D′﹣D′F=4﹣ ![]() .
.
(2)
解:如图②中,
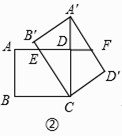
在Rt△A′CD′中,∵∠D′=90°,
∴A′C2=A′D′2+CD′2,
∴A′C=5,A′D=2,
∵∠DA′F=∠CA′D′,∠A′DF=∠D′=90°,
∴△A′DF∽△A′D′C,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴DF= ![]() ,
,
同理可得△CDE∽△CB′A′,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴ED= ![]() ,
,
∴EF=ED+DF= ![]() .
.
(3)
解:如图③中,作FG⊥CB′于G.
∵四边形A′B′CD′是矩形,
∴GF=CD′=CD=3,
∵S△CEF= ![]() EFDC=
EFDC= ![]() CEFG,
CEFG,
∴CE=EF,∵AE=EF,
∴AE=EF=CE,
∴∠ACF=90°,
∵∠ADC=∠ACF,∠CAD=∠FAC,
∴△CAD∽△FAC,
∴ ![]() =
= ![]() ,
,
∴AC2=ADAF,
∴AF= ,
∵S△ACF= ![]() ACCF=
ACCF= ![]() AFCD,
AFCD,
∴ACCF=AFCD= ![]() .
.
【解析】(1)①如图①中,∵矩形ABCD绕点C按顺时针方向旋转α角,得到矩形A'B'C'D',只要证明△CDD′是等边三角形即可解决问题;②如图①中,连接CF,在Rt△CD′F中,求出FD′即可解决问题;(2)由△A′DF∽△A′D′C,可得 ![]() =
= ![]() ,推出DF=
,推出DF= ![]() ,同理可得△CDE∽△CB′A′,由
,同理可得△CDE∽△CB′A′,由 ![]() =
= ![]() ,求出DE,即可解决问题;(3)如图③中,作FG⊥CB′于G,由S△ACF=
,求出DE,即可解决问题;(3)如图③中,作FG⊥CB′于G,由S△ACF= ![]() ACCF=
ACCF= ![]() AFCD,把问题转化为求AFCD,只要证明∠ACF=90°,证明△CAD∽△FAC,即可解决问题;
AFCD,把问题转化为求AFCD,只要证明∠ACF=90°,证明△CAD∽△FAC,即可解决问题;
【考点精析】利用相似三角形的应用和旋转的性质对题目进行判断即可得到答案,需要熟知测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解;①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.


科目:初中数学 来源: 题型:
【题目】如图A在数轴上所对应的数为﹣2.
(1)点B在点A右边距A点4个单位长度,求点B所对应的数;
(2)在(1)的条件下,点A以每秒2个单位长度沿数轴向左运动,点 B 以每秒2个单位长度沿数轴向右运动,当点A运动到﹣6所在的点处时,求A,B两点间距离.
(3)在(2)的条件下,现A点静止不动,B点再以每秒2个单位长度沿数轴向左运动时,经过多长时间A,B两点相距4个单位长度.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题.
 程大位,明代商人,珠算发明家,被称为珠算之父、卷尺之父.少年时,读书极为广博,对数学颇感兴趣,60岁时完成其杰作《直指算法统宗》(简称《算法统宗》).
程大位,明代商人,珠算发明家,被称为珠算之父、卷尺之父.少年时,读书极为广博,对数学颇感兴趣,60岁时完成其杰作《直指算法统宗》(简称《算法统宗》).
在《算法统宗》里记载了一道趣题:一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚各几丁?意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完.试问大、小和尚各多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是我国东汉初年编订的一部数学经典著作![]() 在它的“方程”一章里,一次方程组是由算筹布置而成的
在它的“方程”一章里,一次方程组是由算筹布置而成的![]() 九章算术
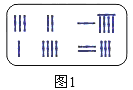
九章算术![]() 中的算筹图是竖排的,为看图方便,我们把它改为横排,如图1、图
中的算筹图是竖排的,为看图方便,我们把它改为横排,如图1、图![]() 图中各行从左到右列出的算筹数分别表示未知数x,y的系数与相应的常数项
图中各行从左到右列出的算筹数分别表示未知数x,y的系数与相应的常数项![]() 把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来,就是
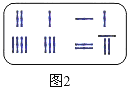
把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来,就是![]() 类似地,图2所示的算筹图我们可以表述为______.
类似地,图2所示的算筹图我们可以表述为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,甲、乙两船同时由港口A出发开往海岛B,甲船沿东北方向向海岛B航行,其速度为15海里/小时;乙船速度为20海里/小时,先沿正东方向航行1小时后,到达C港口接旅客,停留半小时后再转向北偏东30°方向开往B岛,其速度仍为20海里/小时.
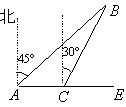
(1)求港口A到海岛B的距离;
(2)B岛建有一座灯塔,在离灯塔方圆5海里内都可以看见灯塔,问甲、乙两船哪一艘先看到灯塔?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】陈老师和学生做一个猜数游戏,他让学生按照如下步骤进行计算:
①任想一个两位数a,把a乘以2,再加上9,把所得的和再乘以2;
②把a乘以2,再加上30,把所得的和除以2;
③把①所得的结果减去②所得的结果,这个差即为最后的结果.
陈老师说:只要你告诉我最后的结果,我就能猜出你最初想的两位数a.
学生周晓晓计算的结果是96,陈老师立即猜出周晓晓最初想的两位数是31.
请完成
(1)由①可列代数式 ,由②可列代数式 ,由③可知最后结果为 ;(用含a的式子表示)
(2)学生小明计算的结果是120,你能猜出他最初想的两位数是多少吗?
(3)请用自己的语言解释陈老师猜数的方法.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学改革学生的学习模式,变“老师要学生学习”为“学生自主学习”,培养了学生自主学习的能力.小华与小明同学就“你最喜欢哪种学习方式”随机调查了他们周围的一些同学,根据收集到的数据绘制了以下两个不完整的统计图(如图).


请根据上面两个不完整的统计图回答以下4个问题:
(1)这次抽样调查中,共调查了_____名学生.
(2)补全条形统计图中的缺项.
(3)在扇形统计图中,选择教师传授的占_____%,选择小组合作学习的占_____%.
(4)根据调查结果,估算该校1800名学生中大约有_____人选择小组合作学习模式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人两次同时在一家粮店购买大米,两次大米的价格分别为每千克a元和b元(a≠b).甲每次买100千克大米,乙每次买100元大米.
(1)用含a、b的代数式表示:甲两次购买大米共需付款 元,乙两次共购买 千克大米.若甲两次购买大米的平均单价为每千克Q1元,乙两次购买大米的平均单价为每千克Q2元.则:Q1= ;Q2= .
(2)若规定谁两次购粮的平均价格低,谁购粮的方式就更合理,请你判断比较甲、乙两人的购粮方式,哪一个更合理,并说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新农村实行大面积机械化种植,为了更好地收割庄稼,农田承包大户张大叔决定购买8台收割机,现有久保田和春雨两种品牌的收割机,其中每台收割机的价格、每天的收割面积如下表![]() 销售商又宣传说,购买一台久保田收割机比购买一台春雨收割机多8万元,购买2台久保田收割机比购买3台春雨收割机多4万元.
销售商又宣传说,购买一台久保田收割机比购买一台春雨收割机多8万元,购买2台久保田收割机比购买3台春雨收割机多4万元.
久保田收割机 | 春雨收割机 | |
价格 | x | y |
收割面积 | 24 | 18 |
![]() 求两种收割机的价格;
求两种收割机的价格;
![]() 如果张大叔购买收割机的资金不超过125万元,那么有哪几种购买方案?
如果张大叔购买收割机的资金不超过125万元,那么有哪几种购买方案?
![]() 在
在![]() 的条件下,若每天要求收割面积不低于150亩,为了节约资金,那么有没有一种最佳购买方案呢?
的条件下,若每天要求收割面积不低于150亩,为了节约资金,那么有没有一种最佳购买方案呢?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com