
 重合),过动点P作PD∥BA交AC于点D.
重合),过动点P作PD∥BA交AC于点D. x,
x, x,而PD=x•sin60°=
x,而PD=x•sin60°= x,
x, PD•AD=
PD•AD=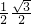 x•(12-
x•(12- x)=-
x)=- (x2-24x)
(x2-24x) (x-12)2+18
(x-12)2+18 .
. <0,
<0, ,
, .
.
 ,O1E=24-3-x=21-x,
,O1E=24-3-x=21-x, )2,
)2, x,
x, x,而PD=x•sin60°=
x,而PD=x•sin60°= x,∴S△APD=
x,∴S△APD= PD•AD把PD,AD的值代入,得到S△APD=-
PD•AD把PD,AD的值代入,得到S△APD=- (x-12)2+18
(x-12)2+18 .
. .
. ,O1E=21-x,
,O1E=21-x, )2,求解得到x的值,进而求得BP的值.
)2,求解得到x的值,进而求得BP的值.

科目:初中数学 来源: 题型:
 (2013•莆田质检)如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,点E是AB上一点,以AE为直径的⊙O过点D,且交AC于点F.
(2013•莆田质检)如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,点E是AB上一点,以AE为直径的⊙O过点D,且交AC于点F.查看答案和解析>>
科目:初中数学 来源: 题型:
 边上移动,使这个30°角的两边分别与△ABC的边AC、BC相交于点E、F,且使DE始终与AB垂直.
边上移动,使这个30°角的两边分别与△ABC的边AC、BC相交于点E、F,且使DE始终与AB垂直.查看答案和解析>>
科目:初中数学 来源: 题型:
| 5 |
 点P与点A不重合时,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M落在线段AC上.设点P的运动时间为t(s).
点P与点A不重合时,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M落在线段AC上.设点P的运动时间为t(s).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com