在3×5的棋盘上.一枚棋子每次可以沿水平或者垂直方向移动一小格.但不可以沿任何斜对角线移动.从某些待定的格子开始.要求棋子经过全部的小正方格恰好一次.但不必回到原来出发的小方格上.在这15个小方格中.有个可以是这枚棋子出发的小方格.A．6 B．8C．9D．10 题目和参考答案——青夏教育精英家教网—

在3×5的棋盘上，一枚棋子每次可以沿水平或者垂直方向移动一小格，但不可以沿任何斜对角线移动.从某些待定的格子开始，要求棋子经过全部的小正方格恰好一次，但不必回到原来出发的小方格上.在这15个小方格中，有( )个可以是这枚棋子出发的小方格.

A．6

B．8

C．9

D．10

3×5的棋盘可以看成是一个横3竖5或横5竖3的方格排布，要使棋子经过全部的小正方格恰好一次，但不必回到原来出发的小方格上，而且棋子每次只能沿水平或者垂直方向移动一小格，所以棋子只能从边缘出发，棋盘又是相互对称的，所以可以出发的小方格为3+5=8个。

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源：不详 题型：解答题

在某市开展城乡综合治理的活动中，需要将A、B、C三地的垃圾50立方米、40立方米、50立方米全部运往垃圾处理场D、E两地进行处理. 已知运往D地的数量比运往E地的数量的2倍少l0立方来．
小题1:求运往D、E两地的数量各是多少立方米?
小题2:若A地运往D地

立方米(

为整数)， B地运往D地30立方米. C地运往D地的数量小于A地运往D地的2倍．其余全部运往E地．且C地运往E地不超过 l2立方米．则A、C两地运往D、E两地有哪几种方案?

查看答案和解析>>

科目：初中数学 来源：不详 题型：填空题

潜水艇原停在海面下650米，先上浮200米，又下潜150米，这时潜水艇在海面下　　　　米处．

查看答案和解析>>

科目：初中数学 来源：不详 题型：单选题

观察下列正方形的四个顶点所标的数字规律,那么2011这个数标在【】

A．第502个正方形的左上角	B．第503个正方形的左上角
C．第502个正方形的右上角	D．第503个正方形的右上角

查看答案和解析>>

科目：初中数学 来源：不详 题型：单选题

如图，将一正方形纸片按下列顺序折叠，然后将最后折叠的纸片沿虚线剪去小扇形，将纸片展开，得到的图形是（）

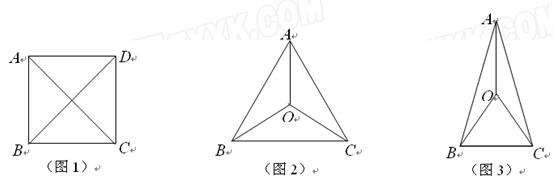
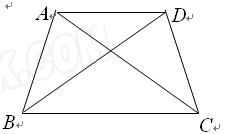
查看答案和解析>>

科目：初中数学 来源：不详 题型：解答题

.用一副三角板，可以画出那些度数的角？

查看答案和解析>>

科目：初中数学 来源：不详 题型：解答题

（8分）在平面上有且只有4个点，这4个点中有一个独特的性质：连结每两点可得到6条线段，这6条线段有且只有两种长度．我们把这四个点称作准等距点．例如正方形ABCD的四个顶点(如图1)，有AB=BC=CD=DA，AC=BD．其实满足这样性质的图形有很多，如图2中A、B、C、O四个点，满足AB=BC=CA，OA=OB=OC；如图3中A、B、C、O四个点，满足OA=OB=OC=BC，AB=AC．