练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】(2016浙江省舟山市第9题)如图，矩形ABCD中，AD=2，AB=3，过点A，C作相距为2的平行线段AE，CF，分别交CD，AB于点E，F，则DE的长是（ ）

    A． B． C．1 D．

    【答案】D

    【解析】

    试题分析：过F作FH⊥AE于H，根据矩形的性质得到AB=CD，AB∥CD，推出四边形AECF是平行四边形，根据平行四边形的性质得到AF=CE，根据相似三角形的性质得到，于是得到AE=AF，列方程即可得到结论．过F作FH⊥AE于H，∵四边形ABCD是矩形，∴AB=CD，AB∥CD，∵AE∥CF，

    ∴四边形AECF是平行四边形，∴AF=CE，∴DE=BF，∴AF=3﹣DE，∴AE=，

    ∵∠FHA=∠D=∠DAF=90°，∴∠AFH+∠HAF=∠DAE+∠FAH=90°，∴∠DAE=∠AFH，

    ∴△ADE∽△AFH，∴，∴AE=AF，∴AE==3﹣DE，∴DE=，

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图是一根可伸缩的鱼竿，鱼竿是用10节大小不同的空心套管连接而成．闲置时鱼竿可收缩，完全收缩后，鱼竿长度即为第1节套管的长度（如图1所示）：使用时，可将鱼竿的每一节套管都完全拉伸（如图2所示）．图3是这跟鱼竿所有套管都处于完全拉伸状态下的平面示意图．已知第1节套管长50cm，第2节套管长46cm，以此类推，每一节套管均比前一节套管少4cm．完全拉伸时，为了使相邻两节套管连接并固定，每相邻两节套管间均有相同长度的重叠，设其长度为xcm．

    （1）请直接写出第5节套管的长度；

    （2）当这根鱼竿完全拉伸时，其长度为311cm，求x的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】观察下列算式：21=2，22=4，23=8，24=16，25=32，26=64，27=128，28=256，…，通过观察，用所发现的规律确定22017的个位数字是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

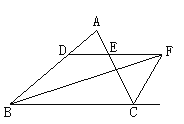
    【题目】如图所示：∠ABC的平分线BF与△ABC中∠ACB的相邻外角的平分线CF相交于点F，过F作DF∥BC，交AB于D，交AC于E．

    问：（1）图中有几个等腰三角形？为什么？

    （2）BD，CE，DE之间存在着什么关系？请证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

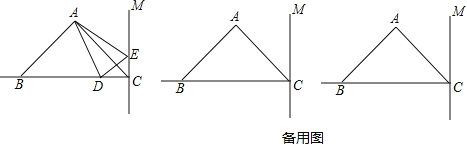
    【题目】如图，在△ABC中，已知AB=AC，∠BAC=90°，BC=10cm，直线CM⊥BC，动点D从点C开始沿射线CB方向以每秒3厘米的速度运动，动点E也同时从点C开始在直线CM上以每秒2厘米的速度运动，连接AD、AE，设运动时间为t秒．

    （1）求AB的长；（2）当t为多少时，△ABD的面积为15cm2？

    （3）当t为多少时，△ABD≌△ACE，并简要说明理由．（请在备用图中画出具体图形）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一组数据2、5、4、3、5、4、5的中位数和众数分别是（　　）
    A.3.5，5
    B.4，4
    C.4，5
    D.4.5，4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知a，b，c是三角形ABC的三边，且b2+2ab=c2+2ac，则三角形ABC的形状是三角形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】(2016湖南省岳阳市第24题)如图①，直线y=x+4交于x轴于点A，交y轴于点C，过A、C两点的抛物线F1交x轴于另一点B（1，0）．

    （1）求抛物线F1所表示的二次函数的表达式；

    （2）若点M是抛物线F1位于第二象限图象上的一点，设四边形MAOC和△BOC的面积分别为S四边形MAOC和S△BOC，记S=S四边形MAOC﹣S△BOC，求S最大时点M的坐标及S的最大值；

    （3）如图②，将抛物线F1沿y轴翻折并“复制”得到抛物线F2，点A、B与（2）中所求的点M的对应点分别为A′、B′、M′，过点M′作M′E⊥x轴于点E，交直线A′C于点D，在x轴上是否存在点P，使得以A′、D、P为顶点的三角形与△AB′C相似？若存在，请求出点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB∥CD，点G、E、F分别在AB、CD上，FG平分∠CFE，若∠1=40°，求∠FGE的度数．

    查看答案和解析>>

    同步练习册答案