
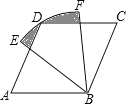
【题目】如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形EBF的半径为2,圆心角为60°,则图中阴影部分的面积是 .
【答案】![]() ﹣
﹣![]() .
.
【解析】
试题分析:根据菱形的性质得出△DAB是等边三角形,进而利用全等三角形的判定得出△ABG≌△DBH,得出四边形GBHD的面积等于△ABD的面积,进而求出即可.
解:如图,连接BD.
∵四边形ABCD是菱形,∠A=60°,
∴∠ADC=120°,
∴∠1=∠2=60°,
∴△DAB是等边三角形,
∵AB=2,
∴△ABD的高为![]() ,
,
∵扇形BEF的半径为2,圆心角为60°,
∴∠4+∠5=60°,∠3+∠5=60°,
∴∠3=∠4,
设AD、BE相交于点G,设BF、DC相交于点H,
在△ABG和△DBH中,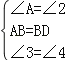 ,
,
∴△ABG≌△DBH(ASA),
∴四边形GBHD的面积等于△ABD的面积,
∴图中阴影部分的面积是:S扇形EBF﹣S△ABD=![]() ﹣
﹣![]() ×2×
×2×![]() =
=![]() ﹣
﹣![]() .
.
故答案是:![]() ﹣
﹣![]() .
.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:
【题目】已知某学校有(5a2+4a+1)名学生正在参加植树活动,为了支援兄弟学校,决定从该校抽调(5a2+7a)名学生去支援兄弟学校,则剩余的学生人数是( )
A. -3a-1 B. -3a+1 C. -11a+1 D. 11a-1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,对于图中标记的各角,下列条件能够推理得到a∥b的是( )
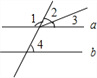
A. ∠1=∠4 B. ∠2=∠4 C. ∠3+∠2=∠4 D. ∠2+∠3+∠4=180°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,二次函数y=ax2+bx+c(a≠0)的图象的对称轴是直线x=1,且经过点(0,2).有下列结论:
①ac>0;②b2﹣4ac>0;③a+c<2﹣b;④a<﹣![]() ;⑤x=﹣5和x=7时函数值相等.
;⑤x=﹣5和x=7时函数值相等.
其中正确的结论有( )
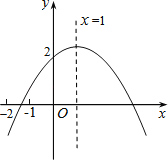
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
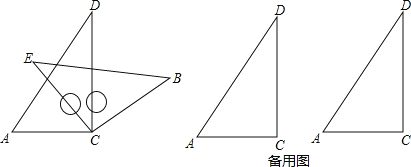
【题目】将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起(其中,∠A=60°,∠D=30°;∠E=∠B=45°):
(1)①若∠DCE=45°,则∠ACB的度数为 ;
②若∠ACB=140°,求∠DCE的度数;
(2)由(1)猜想∠ACB与∠DCE的数量关系,并说明理由.
(3)当∠ACE<180°且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请直接写出∠ACE角度所有可能的值(不必说明理由);若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,AB=AC.D,E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF,下列结论:
①△AED≌△AEF;
②△ABE∽△ACD;
③BE+DC=DE;
④BE2+DC2=DE2.
其中正确的是( )

A.②④ B.①④ C.②③ D.①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读,然后解答提出的问题:
设a,b是有理数,且满足a+![]() b=3﹣2
b=3﹣2![]() ,求ba的值.
,求ba的值.
解:由题意得(a﹣3)+(b+2)![]() =0,因为a,b都是有理数,所以a﹣3,b+2也是有理数,
=0,因为a,b都是有理数,所以a﹣3,b+2也是有理数,
由于![]() 是无理数,所以a﹣3=0,b+2=0,所以a=3,b=﹣2,所以ba=(﹣2)3=﹣8.问题:设x,y都是有理数,且满足x2﹣2y+
是无理数,所以a﹣3=0,b+2=0,所以a=3,b=﹣2,所以ba=(﹣2)3=﹣8.问题:设x,y都是有理数,且满足x2﹣2y+![]() y=8+4
y=8+4![]() ,求x+y的值.
,求x+y的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com