
 ,现将△DEF沿直线BC以每秒
,现将△DEF沿直线BC以每秒 个单位向右平移,直至E点与C点重合时停止运动,设运动时间为t秒.
个单位向右平移,直至E点与C点重合时停止运动,设运动时间为t秒. ?若存在,试求出CH的值;若不存在,请说明理由.
?若存在,试求出CH的值;若不存在,请说明理由.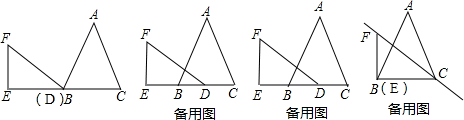
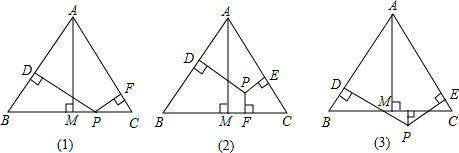
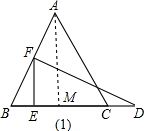 解:(1)当F在边AB上时,如图(1),作AM⊥BC,则AM=
解:(1)当F在边AB上时,如图(1),作AM⊥BC,则AM= AB=
AB= ×6
×6 =9,
=9,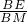 =
= ,即
,即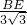 =
=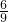 ,解得:BE=2
,解得:BE=2 ,则移动的距离是:6
,则移动的距离是:6 +2
+2 =8
=8 ,则t=
,则t=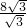 =8;
=8; ,则移动的距离是:2×6
,则移动的距离是:2×6 -2
-2 =12
=12 -2
-2 =10
=10 ,
, 则t=
则t= =10,
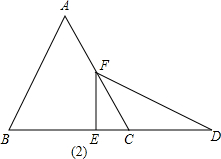
=10,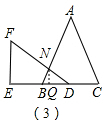 设AB与BE交于点N,
设AB与BE交于点N, t,
t, BD=
BD= t,ND=
t,ND= BD=
BD= ×
× t=
t= t,则s=
t,则s= NB•ND=
NB•ND= ×
× t×
t× t=
t= t2;
t2; (6-t)2 sin30°•cos30°
(6-t)2 sin30°•cos30° (6-t)2,
(6-t)2, t-9,
t-9, -
- (6-t)2-
(6-t)2- t+9=-
t+9=- t2+
t2+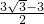 t+
t+ +9,
+9,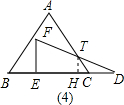 则CD=
则CD= t-6
t-6 ,
, t-6
t-6 ,
, TC=
TC= (
( t-6
t-6 )=
)= t-9,
t-9, -
- CD•TH=18
CD•TH=18 -
- (
( t-6
t-6 )(
)( t-9)=-
t-9)=- (t-6)2+18
(t-6)2+18 ;
;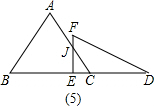
 -
- t,
t, EC=
EC= (12
(12 -
- t),
t), EC•EJ=
EC•EJ= ×
× (12
(12 -
- t)2=
t)2= (12-t)2.
(12-t)2. ×
× =6,
=6, x,
x, x2,
x2, BC•HL=3
BC•HL=3 ×
× x=
x=
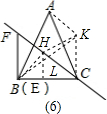 x,
x, x.
x. x-
x- x-
x- x2=4
x2=4 ,方程无解.
,方程无解. x2+
x2+ x-3
x-3 x=4
x=4 ,解得:x=8或-2(舍去),故x=8
,解得:x=8或-2(舍去),故x=8

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
| 3 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com