
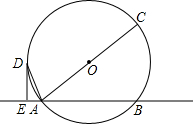
 如图,直线EF交⊙O于A,B两点,AC是⊙O直径,DE是⊙O的切线,且DE⊥EF,垂足为E.
如图,直线EF交⊙O于A,B两点,AC是⊙O直径,DE是⊙O的切线,且DE⊥EF,垂足为E.分析 (1)连接OD,得出∠OAD=∠ODA,再证明∠EAD=∠ODA,得出结论;
(2)首先求得∠EAD=∠ODA=75°,进一步得出∠DOA=30°,利用弧长计算公式得出答案即可;
(3)作OF⊥AB于点F,求得∠OAB=30°,利用含30°角的直角三角形、勾股定理和垂径定理得出答案即可.
解答 (1)证明:如图,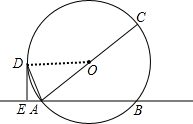
连接OD,
∵OD=OA,
∴∠ODA=∠OAD,
∵DE是⊙O的切线,
∴∠ODE=90°,OD⊥DE,
又∵DE⊥EF,
∴OD∥EF,
∴∠ODA=∠DAE,
∴∠DAE=∠OAD,
∴AD平分∠CAE;
(2)解:∵∠ADE=15°,
∴∠OAD=∠ODA=75°,
∵OD=OA,
∴∠ODA=∠OAD=75°,
∴∠DOA=30°,
∴$\frac{30π×OA}{360}$=$\frac{1}{3}$π,
∴OA=4;
(3)解:如图,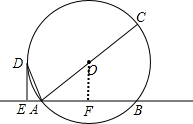
作OF⊥AB于点F,
则AF=FB,
∵∠OAD=∠ODA=75°,
∴∠OAF=30°,
∴OF=2,
AF=$\sqrt{O{A}^{2}-O{F}^{2}}$=2$\sqrt{3}$,
∴AB=2AF=4$\sqrt{3}$.
点评 此题考查切线的性质,等腰三角形的性质,弧长计算公式,垂径定理,含30°直角三角形的性质,勾股定理,正确做出辅助线是解决问题的关键.


科目:初中数学 来源:2016-2017学年广东省东莞市堂星晨学校八年级3月月考数学试卷(解析版) 题型:解答题
若一件商品的进价为500元,标价为750元,商店要求以利润率不低于5%的售价打折出售,设打x折,那么列出的不等式为_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
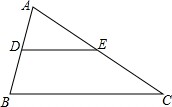 如图,在△ABC中,点D、E分别在AB、AC上,且DE∥BC.
如图,在△ABC中,点D、E分别在AB、AC上,且DE∥BC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
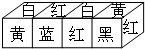 在正方体的六个面上分别涂上红、黄、蓝、白、黑、绿六种颜色,现有涂色方式完全相同的四个正方体,按照如图所示拼成一个长方体,那么涂黄、白两种颜色的面的对面分别涂有( )颜色.
在正方体的六个面上分别涂上红、黄、蓝、白、黑、绿六种颜色,现有涂色方式完全相同的四个正方体,按照如图所示拼成一个长方体,那么涂黄、白两种颜色的面的对面分别涂有( )颜色.| A. | 蓝、红 | B. | 蓝、黑 | C. | 蓝、绿 | D. | 绿、白 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在等腰梯形ABCD中,AB∥CD,点E在对角线AC上,且∠1=∠2,AB=5,BC=AD=$\sqrt{10}$,CD=3.
如图,在等腰梯形ABCD中,AB∥CD,点E在对角线AC上,且∠1=∠2,AB=5,BC=AD=$\sqrt{10}$,CD=3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com