
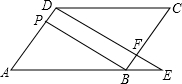
 如图,在?ABCD中,F是BC上的一点,直线DF与AB的延长线相交于点E,BP∥DF,且与AD相交于点P,CD=10,AD=8,PD=2,则BE=$\frac{10}{3}$.
如图,在?ABCD中,F是BC上的一点,直线DF与AB的延长线相交于点E,BP∥DF,且与AD相交于点P,CD=10,AD=8,PD=2,则BE=$\frac{10}{3}$.  巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{4}$$+\sqrt{(-2)^{2}}$=0 | B. | $\sqrt{\frac{3}{2}}$$-\sqrt{\frac{2}{3}}$=0 | C. | $\sqrt{6}$$÷\sqrt{3}$=2 | D. | $\sqrt{6}$×$\sqrt{\frac{3}{2}}$=3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
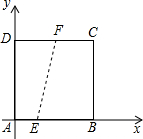 如图,已知正方形ABCD的边长为4,点E在边AB上,且AE=1;点F为边CD上一动点,且DF=m.以A为原点,AB所在直线为x轴建立平面直角坐标系.
如图,已知正方形ABCD的边长为4,点E在边AB上,且AE=1;点F为边CD上一动点,且DF=m.以A为原点,AB所在直线为x轴建立平面直角坐标系.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
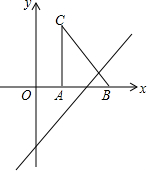 如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=10,点A、B的坐标分别为(2,0)、(8,0),将△ABC沿x轴向右平移,当点C落在直线y=x-5上时,线段BC扫过的面积为( )
如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=10,点A、B的坐标分别为(2,0)、(8,0),将△ABC沿x轴向右平移,当点C落在直线y=x-5上时,线段BC扫过的面积为( )| A. | 80 | B. | 88 | C. | 96 | D. | 100 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
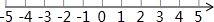
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
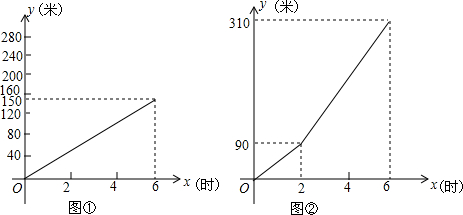
 自从上次赛跑乌龟大胜兔子后,乌龟便成了体育界的名人,又是广告,又是讲演,活动不断,可蚂蚁偏偏不服气,向乌龟下了挑战书,我们来看:
自从上次赛跑乌龟大胜兔子后,乌龟便成了体育界的名人,又是广告,又是讲演,活动不断,可蚂蚁偏偏不服气,向乌龟下了挑战书,我们来看:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
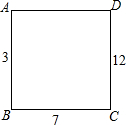 如图,在正方形ABCD的每个顶点上写一个数,把这个正方形每条边的两端点上的数加起来,将和写在这条边上,已知AB上的数是3,BC上的数是7,CD上的数是12,则AD上的数是( )
如图,在正方形ABCD的每个顶点上写一个数,把这个正方形每条边的两端点上的数加起来,将和写在这条边上,已知AB上的数是3,BC上的数是7,CD上的数是12,则AD上的数是( )| A. | 2 | B. | 7 | C. | 8 | D. | 15 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com