
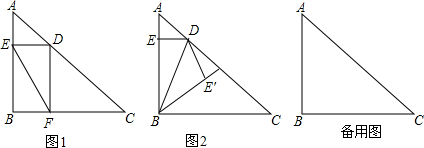
| 3 |
| 3 |
| 4x2-10x+25 |
| 3 |
| 3 |
| 3 |
| DF |
| AP |
| FG |
| GP |
| DG |
| GA |
| 5 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
| BF2+BE2 |
| 4x2-10x+25 |
| 3 |
| 3 |
| 3 |
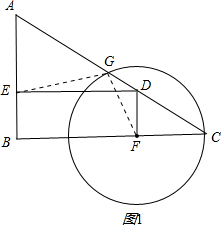 方法1:
方法1:| 3 |
| 3 |
| 5 |
| 2 |
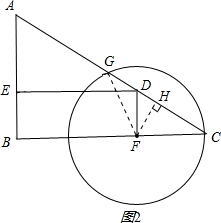
| ||
| 2 |
| 15-3x |
| 2 |
| 5 |
| 2 |
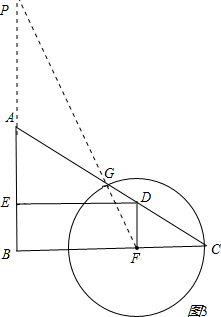 ∵DF∥PB,
∵DF∥PB,| DF |
| AP |
| FG |
| GP |
| DG |
| GA |
| 3 |
| 3 |
| 5 |
| 2 |
| 1800-∠ABD |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
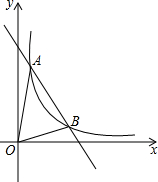 如图,一次函数y=kx+b与反比例函数y=
如图,一次函数y=kx+b与反比例函数y=| 6 |
| x |
| 6 |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 甲 | 乙 | 丙 | 丁 | |
| ∠C(单位:度) | 34 | 36 | 38 | 40 |
. |
| x |
. |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
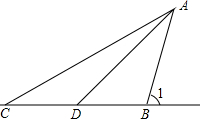 小方与同学一起去郊游,看到一棵大树斜靠在一小土坡上,他想知道树有多长,于是他借来测角仪和卷尺.如图,他在点C处测得树AB顶端A的仰角为30°,沿着CB方向向大树行进10米到达点D,测得树AB顶端A的仰角为45°,又测得树AB倾斜角∠1=75°.
小方与同学一起去郊游,看到一棵大树斜靠在一小土坡上,他想知道树有多长,于是他借来测角仪和卷尺.如图,他在点C处测得树AB顶端A的仰角为30°,沿着CB方向向大树行进10米到达点D,测得树AB顶端A的仰角为45°,又测得树AB倾斜角∠1=75°.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
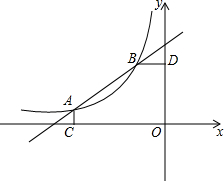 如图,已知A(-4,
如图,已知A(-4,| 1 |
| 2 |
| m |
| x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com