
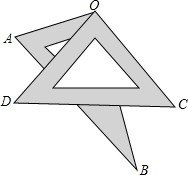
 如图,将一副三角板叠放在一起,使直角顶点重合于O点,则∠AOC+∠BOD=
如图,将一副三角板叠放在一起,使直角顶点重合于O点,则∠AOC+∠BOD=科目:初中数学 来源: 题型:
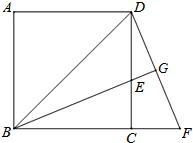 如图,四边形ABCD是正方形,点F在BC延长线上,且BF=BD,G为DF中点,BG与DC交于点E,以下结论正确的有
如图,四边形ABCD是正方形,点F在BC延长线上,且BF=BD,G为DF中点,BG与DC交于点E,以下结论正确的有查看答案和解析>>
科目:初中数学 来源: 题型:
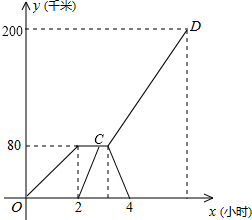 已知A、B两市相距200千米,甲车从A市前往B市运送物资,行驶2小时在M地汽车出现故障不能行驶,立即通知技术人员乘乙车从A市赶去维修(通知时间忽略不计),乙车到达M地后用24分钟修好甲车后以原速度原路返回,同时甲车以原速1.5倍的速度前往B市,如图是两车距A市的路程y(千米)与甲车的行驶时间x(小时)之间的函数图象,结合图象回答下列问题:
已知A、B两市相距200千米,甲车从A市前往B市运送物资,行驶2小时在M地汽车出现故障不能行驶,立即通知技术人员乘乙车从A市赶去维修(通知时间忽略不计),乙车到达M地后用24分钟修好甲车后以原速度原路返回,同时甲车以原速1.5倍的速度前往B市,如图是两车距A市的路程y(千米)与甲车的行驶时间x(小时)之间的函数图象,结合图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
 联欢会上,墙上挂着两串礼物,A、B、C、D、E如图所示,每次从某一串的最下端摘下一个礼物,这样摘了五次可将五件礼物全部摘下,那么共有
联欢会上,墙上挂着两串礼物,A、B、C、D、E如图所示,每次从某一串的最下端摘下一个礼物,这样摘了五次可将五件礼物全部摘下,那么共有查看答案和解析>>
科目:初中数学 来源: 题型:
 小明对自己所在班级的学生平均每周参加课外活动的时间进行了调查,由调查结果的部分数据填在了如下的表格中,并绘制了频数分布直方图,根据图表中信息回答下列问题:
小明对自己所在班级的学生平均每周参加课外活动的时间进行了调查,由调查结果的部分数据填在了如下的表格中,并绘制了频数分布直方图,根据图表中信息回答下列问题:| 活动时间(小时) | 频数 | 频率 |
| 0~2 | m | 0.12 |
| 2~4 | 12 | 0.24 |
| 4~6 | 24 | |
| 6~8 | n | |
| 8~10 | 4 | |
| 合计 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,等腰直角三角形ABC中,AD是底边BC上的高,现将△ABD沿DC方向平移,使点D和点C重合,若重叠部分(阴影部分)的面积是4,则△ABC的腰长为
如图,等腰直角三角形ABC中,AD是底边BC上的高,现将△ABD沿DC方向平移,使点D和点C重合,若重叠部分(阴影部分)的面积是4,则△ABC的腰长为查看答案和解析>>
科目:初中数学 来源: 题型:
 函数y1=
函数y1=| 5 |
| x |
| 5 |
| x |
| 3 |
| x |
| 3 |
| x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com