
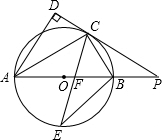
 如图,AB是⊙O的直径,点C是⊙O上一点,AD和过点C的切线互相垂直,垂足为D,直线DC与AB的延长线相交于P.弦CE平分∠ACB,交直径AB于点F,连结BE.
如图,AB是⊙O的直径,点C是⊙O上一点,AD和过点C的切线互相垂直,垂足为D,直线DC与AB的延长线相交于P.弦CE平分∠ACB,交直径AB于点F,连结BE.分析 (1)先判断出∠OAC=∠OCA,再判断出OC∥AD,即可得出结论;
(2)先判断出∠CAD+∠ACD=90°,进而得出∠PFC=∠PCF即可得出结论;
(3)先求出AB=10,再找出3CA=4BC,最后用勾股定理即可得出结论.
解答 解:(1)如图1, 连接OC,
连接OC,
∵OA=OC,
∴∠OAC=∠OCA.
∵PC是⊙O的切线,AD⊥CD,
∴∠OCP=∠D=90°,
∴OC∥AD.
∴∠CAD=∠OCA=∠OAC.
即AC平分∠DAB.
(2)PC=PF.
理由:∵AB是直径,
∴∠ACB=90°,
∴∠PCB+∠ACD=90°
又∵∠CAD+∠ACD=90°,
∴∠CAB=∠CAD=∠PCB.
又∵∠ACE=∠BCE,∠PFC=∠CAB+∠ACE,∠PCF=∠PCB+∠BCE.
∴∠PFC=∠PCF.
∴PC=PF.
(3)如图2, 连接AE.∵∠ACE=∠BCE,
连接AE.∵∠ACE=∠BCE,
∴$\widehat{AE}=\widehat{BE}$,
∴AE=BE.
又∵AB是直径,
∴∠AEB=90°.AB=$\sqrt{2}$BE=10,
∵tan∠CEB=tan∠CAB=$\frac{3}{4}$,
∴$\frac{BC}{CA}$=$\frac{3}{4}$.
设BC=3x,则CA=4x,
在Rt△ABC中,(3x)2+(4x)2=100
解得x=-2(舍)或x=2,
∴BC=6,AC=8.
点评 此题是圆的综合题,主要考查了圆的性质,圆的切线的性质,解平分线的定义,锐角三角函数,勾股定理,解(1)的关键是得出OC∥AD,解(2)的关键是得出∠CAB=∠CAD=∠PCB,解(3)的关键是用勾股定理建立方程,是一道中等难度的中考常考题.


科目:初中数学 来源: 题型:解答题
 (1)计算:($\sqrt{3}$-1)0+2sin30°-($\frac{1}{2}$)-1+|-2017|;
(1)计算:($\sqrt{3}$-1)0+2sin30°-($\frac{1}{2}$)-1+|-2017|;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
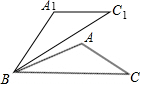
| A. | 底与边不相等的等腰三角形 | B. | 等边三角形 | ||
| C. | 钝角三角形 | D. | 直角三角形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,反比例函数y=$\frac{m}{x}$(x>0)与一次函数y=kx+6$\sqrt{3}$交于点C(2,4$\sqrt{3}$),一次函数图象与两坐标轴分别交于点A和点B,动点P从点A出发,沿AB以每秒1个单位长度的速度向点B运动;同时,动点Q从点O出发,沿OA以相同的速度向点A运动,运动时间为t秒(0<t≤6),以点P为圆心,PA为半径的⊙P与AB交于点M,与OA交于点N,连接MN、MQ.
如图,反比例函数y=$\frac{m}{x}$(x>0)与一次函数y=kx+6$\sqrt{3}$交于点C(2,4$\sqrt{3}$),一次函数图象与两坐标轴分别交于点A和点B,动点P从点A出发,沿AB以每秒1个单位长度的速度向点B运动;同时,动点Q从点O出发,沿OA以相同的速度向点A运动,运动时间为t秒(0<t≤6),以点P为圆心,PA为半径的⊙P与AB交于点M,与OA交于点N,连接MN、MQ.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知:点A(0,2),动点P从点A出发,沿y轴以每秒1个单位长度的速度向上移动,且过点P的直线l:y=-2x+b也随之移动,并与x轴交于点B,设动点P移动时间为t s.
如图,已知:点A(0,2),动点P从点A出发,沿y轴以每秒1个单位长度的速度向上移动,且过点P的直线l:y=-2x+b也随之移动,并与x轴交于点B,设动点P移动时间为t s.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
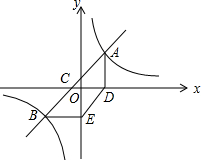 如图,已知双曲线y=$\frac{k}{x}$经过点A(3,$\frac{20}{3}$),点B是双曲线第三象限上的一个动点,过点A作AD⊥x轴于点D,过点B作BE⊥y轴于点E.
如图,已知双曲线y=$\frac{k}{x}$经过点A(3,$\frac{20}{3}$),点B是双曲线第三象限上的一个动点,过点A作AD⊥x轴于点D,过点B作BE⊥y轴于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com