
 ��ͼ������������y=$\frac{m}{x}$��x��0����һ�κ���y=kx+6$\sqrt{3}$���ڵ�C��2��4$\sqrt{3}$����һ�κ���ͼ������������ֱ��ڵ�A�͵�B������P�ӵ�A��������AB��ÿ��1����λ���ȵ��ٶ����B�˶���ͬʱ������Q�ӵ�O��������OA����ͬ���ٶ����A�˶����˶�ʱ��Ϊt�루0��t��6�����Ե�PΪԲ�ģ�PAΪ�뾶�ġ�P��AB���ڵ�M����OA���ڵ�N������MN��MQ��
��ͼ������������y=$\frac{m}{x}$��x��0����һ�κ���y=kx+6$\sqrt{3}$���ڵ�C��2��4$\sqrt{3}$����һ�κ���ͼ������������ֱ��ڵ�A�͵�B������P�ӵ�A��������AB��ÿ��1����λ���ȵ��ٶ����B�˶���ͬʱ������Q�ӵ�O��������OA����ͬ���ٶ����A�˶����˶�ʱ��Ϊt�루0��t��6�����Ե�PΪԲ�ģ�PAΪ�뾶�ġ�P��AB���ڵ�M����OA���ڵ�N������MN��MQ������ ��1�����ô���ϵ����ֱ�����m��k��
��2�������AB�������жϳ���MAN�ס�BAO�����ñ���ʽ�ó�AN��MN�����ɵó�ON������ON=OQ����������⼴�ɣ�
��3��������������������ε������ʽ���ɵó����ۣ�
��� �⣺��1����C��2��4$\sqrt{3}$������y=$\frac{m}{x}$�еã�m=8$\sqrt{3}$
����2��3$\sqrt{3}$������y=kx+6$\sqrt{3}$�еã�2k+6$\sqrt{3}$=4$\sqrt{3}$
��k=-$\sqrt{3}$
��2���ɣ�1��֪��k=-$\sqrt{3}$��
��ֱ��AB�Ľ���ʽΪy=-$\sqrt{3}$x+6$\sqrt{3}$��
��A��6��0����B��0��6$\sqrt{3}$����
��AB=12
��AM��ֱ��
���ANM=90�㣬
���ANM=��AOB
�֡ߡ�MAN=��BAO��
���MAN�ס�BAO��
��$\frac{AN}{AO}=\frac{MN}{BO}=\frac{AM}{AB}$
��OQ=AP=t��AM=2AP=2t��OA=6��OB=6$\sqrt{3}$��AB=12
��$\frac{AN}{6}=\frac{MN}{6\sqrt{3}}=\frac{2t}{12}$
��AN=t��MN=$\sqrt{3}$t
��ON=OA-AN=6-t
�ߵ�Q���N�غ�
��ON=OQ
��6-t=t
��t=3
��3���ٵ�0��t��3ʱ��QN=OA-OQ-AN=6-2t
��S=$\frac{1}{2}$QN•MN=$\frac{1}{2}$��6-2t��•$\sqrt{3}$t=-$\sqrt{3}$t2+3$\sqrt{3}$t
�ڵ�3��t��6ʱ��QN=OQ+NA-OA=t+t-6=2t-6
��S=$\frac{1}{2}$QN•MN=$\frac{1}{2}$��2t-6��•$\sqrt{3}$t=$\sqrt{3}$t2-3$\sqrt{3}$t��
����S=$\left\{\begin{array}{l}{-\sqrt{3}{t}^{2}+3\sqrt{3}t��0��t��3��}\\{\sqrt{3}{t}^{2}-3\sqrt{3}t��3��t��6��}\end{array}\right.$
���� �����Ƿ����������ۺ��⣬��Ҫ�����˴���ϵ���������������ε��ж������ʣ������ε������ʽ�����÷���˼�������⣬�⣨2���Ĺؼ����������������ε��������AN��MN����һ���е��Ѷȵ��п������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a��-$\frac{2}{3}$ | B�� | a��2 | C�� | a��-$\frac{2}{3}$ | D�� | a��2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
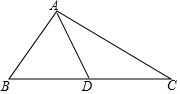 ��ͼ����ABC�У�AD�����ߣ���BAD=��B+��C��tan��ABC=$\frac{11}{10}$����tan��BAD=$\frac{33}{10}$��
��ͼ����ABC�У�AD�����ߣ���BAD=��B+��C��tan��ABC=$\frac{11}{10}$����tan��BAD=$\frac{33}{10}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
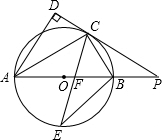 ��ͼ��AB�ǡ�O��ֱ������C�ǡ�O��һ�㣬AD����C�������ഹֱ������ΪD��ֱ��DC��AB���ӳ����ཻ��P����CEƽ�֡�ACB����ֱ��AB�ڵ�F������BE��
��ͼ��AB�ǡ�O��ֱ������C�ǡ�O��һ�㣬AD����C�������ഹֱ������ΪD��ֱ��DC��AB���ӳ����ཻ��P����CEƽ�֡�ACB����ֱ��AB�ڵ�F������BE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
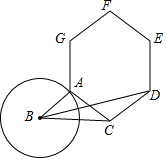 ��ͼ��BC=2��AΪ�뾶Ϊ1�ġ�B��һ�㣬����AC����AC�Ϸ���һ����������ACDEFG������BD����BD�����ֵΪ$2\sqrt{3}+1$��
��ͼ��BC=2��AΪ�뾶Ϊ1�ġ�B��һ�㣬����AC����AC�Ϸ���һ����������ACDEFG������BD����BD�����ֵΪ$2\sqrt{3}+1$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ת��ת�̵Ĵ���n | 100 | 150 | 200 | 500 | 800 | 1000 |
| ���ڡ�Ǧ�ʡ��Ĵ���m | 68 | 111 | 136 | 345 | 564 | 701 |
| ���ڡ�Ǧ�ʡ���Ƶ�� $\frac{m}{n}$ | 0.68 | 0.74 | 0.68 | 0.69 | 0.705 | 0.701 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com