
| 转动转盘的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
| 落在“铅笔”的次数m | 68 | 111 | 136 | 345 | 564 | 701 |
| 落在“铅笔”的频率 $\frac{m}{n}$ | 0.68 | 0.74 | 0.68 | 0.69 | 0.705 | 0.701 |
分析 (1)根据频率公式可以计算空格要填的数据;
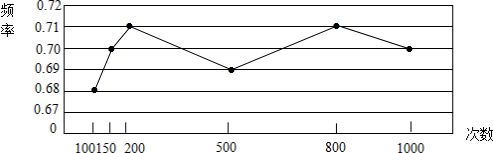
(2)根据(1)中所求,得出获得“三等奖”频率的折线统计图即可;
(3)根据计算出的频率求出平均值即为转盘的次数n很大概率的接近值..
解答 解:(1)
| 转动转盘的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
| 落在“铅笔”的次数m | 68 | 111 | 136 | 345 | 564 | 701 |
| 落在“铅笔”的频率 | 0.68 | 0.74 | 0.68 | 0.69 | 0.705 | 0.701 |
点评 本题考查的是利用频率估计概率,正确理解频率与概率之间的关系是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
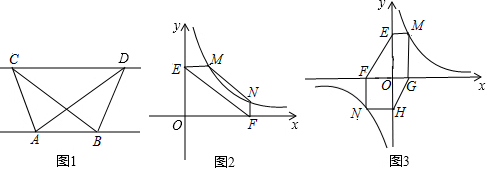
 如图,反比例函数y=$\frac{m}{x}$(x>0)与一次函数y=kx+6$\sqrt{3}$交于点C(2,4$\sqrt{3}$),一次函数图象与两坐标轴分别交于点A和点B,动点P从点A出发,沿AB以每秒1个单位长度的速度向点B运动;同时,动点Q从点O出发,沿OA以相同的速度向点A运动,运动时间为t秒(0<t≤6),以点P为圆心,PA为半径的⊙P与AB交于点M,与OA交于点N,连接MN、MQ.
如图,反比例函数y=$\frac{m}{x}$(x>0)与一次函数y=kx+6$\sqrt{3}$交于点C(2,4$\sqrt{3}$),一次函数图象与两坐标轴分别交于点A和点B,动点P从点A出发,沿AB以每秒1个单位长度的速度向点B运动;同时,动点Q从点O出发,沿OA以相同的速度向点A运动,运动时间为t秒(0<t≤6),以点P为圆心,PA为半径的⊙P与AB交于点M,与OA交于点N,连接MN、MQ.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知:点A(0,2),动点P从点A出发,沿y轴以每秒1个单位长度的速度向上移动,且过点P的直线l:y=-2x+b也随之移动,并与x轴交于点B,设动点P移动时间为t s.
如图,已知:点A(0,2),动点P从点A出发,沿y轴以每秒1个单位长度的速度向上移动,且过点P的直线l:y=-2x+b也随之移动,并与x轴交于点B,设动点P移动时间为t s.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
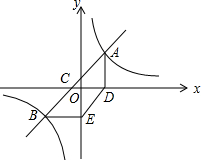 如图,已知双曲线y=$\frac{k}{x}$经过点A(3,$\frac{20}{3}$),点B是双曲线第三象限上的一个动点,过点A作AD⊥x轴于点D,过点B作BE⊥y轴于点E.
如图,已知双曲线y=$\frac{k}{x}$经过点A(3,$\frac{20}{3}$),点B是双曲线第三象限上的一个动点,过点A作AD⊥x轴于点D,过点B作BE⊥y轴于点E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=$\frac{2}{x}$ | B. | y=$\frac{-2}{x}$ | C. | y=-2x+4 | D. | y=4+2x |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com