
【题目】已知点A(-2,n)在抛物线![]() 上.
上.
(1)若b=1,c=3,①求n的值;
②求出此时二次函数在![]() 上的最小值
上的最小值
(2)若此抛物线经过点B(6,n),且二次函数![]() 的最小值是-4,请画出点P(
的最小值是-4,请画出点P(![]() ,
, ![]() )的纵坐标随横坐标变化的图象,并说明理由.
)的纵坐标随横坐标变化的图象,并说明理由.
【答案】(1)①5; ②3; (2)图象见解析,理由见解析;
【解析】分析:(1)代入b=1,c=3,以及A点的坐标即可求得n的值;
(2)由(1)得出y=x+x-3,对称轴为x=![]() ,根据二次函数的增减性可得出结果;
,根据二次函数的增减性可得出结果;
(3)根据题意求得抛物线的解析式为y=(x-2)-4,从而求得点P(x-2,x+bx+c)的纵坐标随横坐标变化的关系式为y=![]() - 4,然后利用5点式画出函数的图象即可.
- 4,然后利用5点式画出函数的图象即可.
本题解析:(1)∵b=1,c=3,
①A(-2,n)在抛物线y=x2+bx+c上.
∴n=4+(-2)×1+3=5.
②当![]() 时,
时,
∵![]()
∴当![]() 时,y随x的增大而增大
时,y随x的增大而增大
∴当x=0时,y取最小值为3
(3)∵此抛物线经过点A(-2,n),B(6,n),
∴抛物线的对称轴x=![]() =2,
=2,
∵二次函数y=x2+bx+c的最小值是-4,
∴抛物线的解析式为y=(x-2)2-4,令x-2=x′,
∴点P(x-2,x2+bx+c)的纵坐标随横坐标变化的关系式为y=![]() - 4,
- 4,
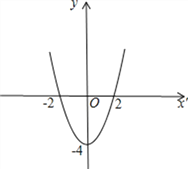
点P(x-2,x2+bx+c)的纵坐标随横坐标变化的如图:


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
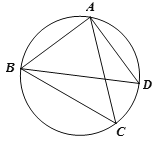
【题目】如图![]() ,点C为△ABD外接圆上的一动点(点C不在
,点C为△ABD外接圆上的一动点(点C不在![]() 上,且不与点B,D重合),∠ACB=∠ABD=45°.
上,且不与点B,D重合),∠ACB=∠ABD=45°.
(1)求证:BD是该外接圆的直径;
(2)连结CD,求证:![]() AC=BC+CD;
AC=BC+CD;
(3)若△ABC关于直线AB的对称图形为△ABM,连接DM,试探究![]() ,
,![]() 三者之间满足的等量关系,并证明你的结论.
三者之间满足的等量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016宁夏第8题)正比例函数y1=k1x的图象与反比例函数y2=![]() 的图象相交于A,B两点,其中点B的横坐标为﹣2,当y1<y2时,x的取值范围是( )
的图象相交于A,B两点,其中点B的横坐标为﹣2,当y1<y2时,x的取值范围是( )
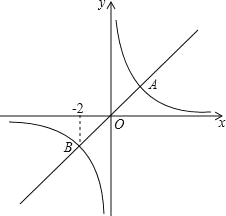
A.x<﹣2或x>2
B.x<﹣2或0<x<2
C.﹣2<x<0或0<x<2
D.﹣2<x<0或x>2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com