
 ��������P��A�㿪ʼ������AO��OB��BA�˶�����P��AO��OB��BA���˶���������q��ѧ��ȤС��Ծ����������˳������飬�ٶȷֱ�Ϊ1��
��������P��A�㿪ʼ������AO��OB��BA�˶�����P��AO��OB��BA���˶���������q��ѧ��ȤС��Ծ����������˳������飬�ٶȷֱ�Ϊ1��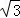 ��2����λ����/�룩��һֱ�ߵ��ϱ�Եl��x���λ�ÿ�ʼ��
��2����λ����/�룩��һֱ�ߵ��ϱ�Եl��x���λ�ÿ�ʼ�� 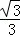 ����λ����/�룩���ٶ�����ƽ���ƶ������ƶ������б���l��x�ᣩ���ҷֱ���OB��AB����E��F����q�趯��P�붯ֱ��lͬʱ�������˶�ʱ��Ϊt�룬����P������AO��OB��BA�˶�һ��ʱ��ֱ��l�Ͷ���Pͬʱֹͣ�˶���
����λ����/�룩���ٶ�����ƽ���ƶ������ƶ������б���l��x�ᣩ���ҷֱ���OB��AB����E��F����q�趯��P�붯ֱ��lͬʱ�������˶�ʱ��Ϊt�룬����P������AO��OB��BA�˶�һ��ʱ��ֱ��l�Ͷ���Pͬʱֹͣ�˶���
 ��
��
 x+3
x+3 ��
�� ����
����  ������������֪����P���E��OB���غϣ�
������������֪����P���E��OB���غϣ� =
= +
+ ����
���� =3+
=3+ ��
�� ��
��  ��
�� =
= ����t=
����t= ��
�� t����A=60�㣬
t����A=60�㣬 t��
t�� t���� t=
t���� t= 
 t��
t�� ��
�� t��
t��
 EF=
EF= ��
�� =
= �����t=
�����t= ��
��




 ��ͼͼ�麮����ҵ������ҵ���ִ�ѧ������ϵ�д�
��ͼͼ�麮����ҵ������ҵ���ִ�ѧ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ��Ķ�����
| 3 |
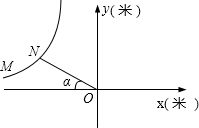 Ϊ��-2250
��-2250| 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ��Ķ�����
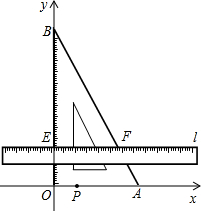 �Ķ����ϣ���ֱ���������У�30�����Ե�ֱ�DZ���б�ߵ�һ�룮
�Ķ����ϣ���ֱ���������У�30�����Ե�ֱ�DZ���б�ߵ�һ�룮| 3 |
| 3 |
| ||
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 9 |
| 2 |
| 9 |
| 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ��Ķ�����
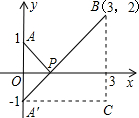 �Ķ����ϣ�
�Ķ����ϣ�| (x2-x2)2(y2-y1)2 |
| x2+1 |
| (x-3)2+4 |
| x2+1 |
| (x-3)2+4 |
| (x-0)2+(0-1)2 |
| (x-3)2+(0-2)2 |
| (x-0)2+(0-1)2 |
| (x-3)2+(0-2)2 |
| 2 |
| 2 |
| 2 |
| 2 |
| (x-i)2+1 |
| (x-2)2+9 |
| x2+49 |
| x2-12x+37 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2011-2012ѧ���㽭ʡ̨��������ʵ��ѧУ���꼶���ϣ�������ѧ�Ծ��������棩 ���ͣ������
 ��������P��A�㿪ʼ������AO-OB-BA�˶�����P��AO��OB��BA���˶����ٶȷֱ�Ϊ1��
��������P��A�㿪ʼ������AO-OB-BA�˶�����P��AO��OB��BA���˶����ٶȷֱ�Ϊ1�� ��2����λ����/�룩��һֱ�ߵ��ϱ�Եl��x���λ�ÿ�ʼ��
��2����λ����/�룩��һֱ�ߵ��ϱ�Եl��x���λ�ÿ�ʼ�� ����λ����/�룩���ٶ�����ƽ���ƶ������ƶ������б���l��x�ᣩ���ҷֱ���OB��AB����E��F����q�趯��P�붯ֱ��lͬʱ�������˶�ʱ��Ϊt�룬����P������AO-OB-BA�˶�һ��ʱ��ֱ��l�Ͷ���Pͬʱֹͣ�˶���
����λ����/�룩���ٶ�����ƽ���ƶ������ƶ������б���l��x�ᣩ���ҷֱ���OB��AB����E��F����q�趯��P�붯ֱ��lͬʱ�������˶�ʱ��Ϊt�룬����P������AO-OB-BA�˶�һ��ʱ��ֱ��l�Ͷ���Pͬʱֹͣ�˶���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com