试题分析:(1)根据基本作图作出∠BAC的角平分线AD交⊙O于点D;点D作AC的垂线,垂足为点E;
(2)连接OD,先根据圆的基本性质可得OA=OD,根据“等边对等角”可得∠OAD=∠ODA,再结合AD平分∠BAC可得∠EAD=∠ODA,即可证得AC∥OD,然后根据平行线的性质即可作出判断;
(3)根据直径所对的圆周角为直角得到∠ADB=90°,而DE⊥AC,则∠AED=90°,又由AD平分∠CAB得到△AED∽△ADB,再根据相似三角形的对应边成比例即可求得结果.
试题解析:(1)如图所示:

(2)连接OD
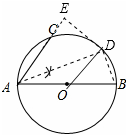
∵OA=OD
∴∠OAD=∠ODA,
∵AD平分∠BAC
∴∠EAD=∠OAD
∴∠EAD=∠ODA
∴AC∥OD
∵DE⊥AC
∴∠EDO=90°
∴DE是⊙O的切线;
(3)∵AB是⊙O的直径,
∴∠ADB=90°,
∵DE⊥AC,
∴∠AED=90°,
∵AD平分∠CAB,
∴∠CAD=∠DAB,
∴Rt△ADE∽Rt△ABD,
∴

∵AD=5,AE=4
∴

,解得

,即⊙O的直径为

.







 ,解得
,解得 ,即⊙O的直径为
,即⊙O的直径为 .
.