
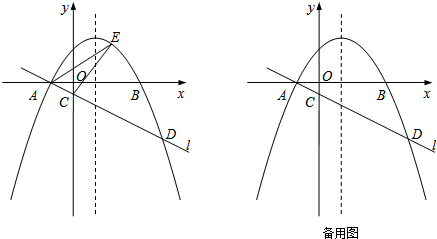
分析 (1)解方程即可得到结论;
(2)根据直线l:y=kx+b过A(-1,0),得到直线l:y=kx+k,解方程得到点D的横坐标为4,求得k=a,得到直线l的函数表达式为y=ax+a;
(3)过E作EF∥y轴交直线l于F,设E(x,ax2-2ax-3a),得到F(x,ax+a),求出EF=ax2-3ax-4a,根据三角形的面积公式列方程即可得到结论;
(4)令ax2-2ax-3a=ax+a,即ax2-3ax-4a=0,得到D(4,5a),设P(1,m),①若AD是矩形ADPQ的一条边,②若AD是矩形APDQ的对角线,列方程即可得到结论.
解答 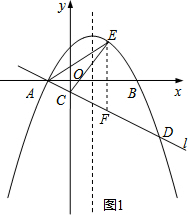 解:(1)当y=0时,ax2-2ax-3a=0,
解:(1)当y=0时,ax2-2ax-3a=0,
解得:x1=-1,x2=3,
∴A(-1,0),B(3,0),
对称轴为直线x=$\frac{-1+3}{2}$=1;
(2)∵直线l:y=kx+b过A(-1,0),
∴0=-k+b,
即k=b,
∴直线l:y=kx+k,
∵抛物线与直线l交于点A,D,
∴ax2-2ax-3a=kx+k,
即ax2-(2a+k)x-3a-k=0,
∵CD=4AC,
∴点D的横坐标为4,
∴-3-$\frac{k}{a}$=-1×4,
∴k=a,
∴直线l的函数表达式为y=ax+a;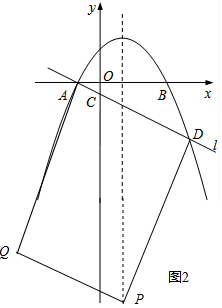
(3)过E作EF∥y轴交直线l于F,设E(x,ax2-2ax-3a),
则F(x,ax+a),EF=ax2-2ax-3a-ax-a=ax2-3ax-4a,
∴S△ACE=S△AFE-S△CEF=$\frac{1}{2}$(ax2-3ax-4a)(x+1)-$\frac{1}{2}$(ax2-3ax-4a)x=$\frac{1}{2}$(ax2-3ax-4a)=$\frac{1}{2}$a(x-$\frac{3}{2}$)2-$\frac{25}{8}$a,
∴△ACE的面积的最大值=-$\frac{25}{8}$a,
∵△ACE的面积的最大值为$\frac{5}{4}$,
∴-$\frac{25}{8}$a=$\frac{5}{4}$,
解得a=-$\frac{2}{5}$;
(4)以点A、D、P、Q为顶点的四边形能成为矩形,
令ax2-2ax-3a=ax+a,即ax2-3ax-4a=0,
解得:x1=1,x2=4,
∴D(4,5a),
∵抛物线的对称轴为直线x=1,
设P(1,m),
①若AD是矩形ADPQ的一条边,
则易得Q(-4,21a),
m=21a+5a=26a,则P(1,26a),
∵四边形ADPQ是矩形,
∴∠ADP=90°,
∴AD2+PD2=AP2,
∴52+(5a)2+32+(26-5a)2=22+(26a)2,
即a2=$\frac{1}{7}$,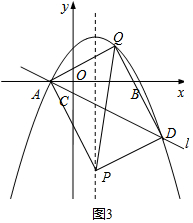
∵a<0,
∴a=-$\frac{\sqrt{7}}{7}$,
∴P(1,-$\frac{26\sqrt{7}}{7}$);
②若AD是矩形APDQ的对角线,
则易得Q(2,-3a),
m=5a-(-3a)=8a,则P(1,8a),
∵四边形APDQ是矩形,
∴∠APD=90°,
∴AP2+PD2=AD2,
∴(-1-1)2+(8a)2+(1-4)2+(8a-5a)2=52+(5a)2,
即a2=$\frac{1}{4}$,
∵a<0,
∴a=-$\frac{1}{2}$,
∴P(1,-4),
综上所述,点A、D、P、Q为顶点的四边形能成为矩形,点P(1,-$\frac{26\sqrt{7}}{7}$)或(1,-4).
点评 本题考查了待定系数法求函数的解析式,三角形面积的计算,平行四边形的性质,勾股定理,正确的作出辅助线是解题的关键.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x(元) | 200 | 240 | 270 | 300 |
| y(间) | 90 | 70 | 55 | 40 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
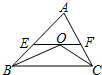 如图,在△ABC中,点O是△ABC的内心,连接OB,OC,过点O作EF∥BC分别交AB,AC于点E,F.已知△ABC的周长为8,BC=x,△AEF的周长为y,则表示y与x的函数图象大致是( )
如图,在△ABC中,点O是△ABC的内心,连接OB,OC,过点O作EF∥BC分别交AB,AC于点E,F.已知△ABC的周长为8,BC=x,△AEF的周长为y,则表示y与x的函数图象大致是( )| A. | 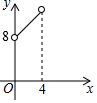 | B. | 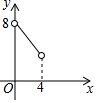 | C. | 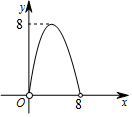 | D. | 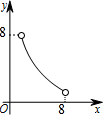 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
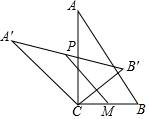 如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C逆时针旋转得到△A'B'C,M是BC的中点,P是A'B'的中点,连接PM.若BC=2,∠BAC=30°,则线段PM的最大值是( )
如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C逆时针旋转得到△A'B'C,M是BC的中点,P是A'B'的中点,连接PM.若BC=2,∠BAC=30°,则线段PM的最大值是( )| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
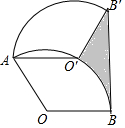 如图,将半径为2,圆心角为120°的扇形OAB绕点A逆时针旋转60°,点O,B的对应点分别为O′,B′,连接BB′,则图中阴影部分的面积是( )
如图,将半径为2,圆心角为120°的扇形OAB绕点A逆时针旋转60°,点O,B的对应点分别为O′,B′,连接BB′,则图中阴影部分的面积是( )| A. | $\frac{2π}{3}$ | B. | 2$\sqrt{3}$-$\frac{π}{3}$ | C. | 2$\sqrt{3}$-$\frac{2π}{3}$ | D. | 4$\sqrt{3}$-$\frac{2π}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com