
如图,直线y=3x+m交x轴于点A,交y轴于点B(0,3),过A、B两点的抛物线交x轴于另一点C(3,0).

(1)求抛物线的解析式;
(2)在该抛物线的对称轴上找一点P,使PA+PB最小,求出点P的坐标;
(3)在抛物线的对称轴上是否存在点Q,使△ABQ是等腰三角形?若存在,求出符合条件的Q点坐标;若不存在,请说明理由.
(1)y=-x2+2x+3.(2)P(1,2),(3)Q1(1,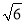 )Q2(1,-
)Q2(1,-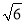 ),Q3(1,0),Q4(1,1).
),Q3(1,0),Q4(1,1).
【解析】
试题分析:(1)由直线y=3x+m交y轴于点B,求出m的值,可得出A的坐标,把A(-1,0),B(0,3),C(3,0)代入y=ax2+bx+c,即可得出抛物线的解析式,
(2)连接BC,交对称轴一点,此点就是点P,使PA+PB最小,求出直线BC的解析式,再利用对称轴为x=1,即可得出点P的坐标,
(3)利用①当AQ=AB时,△ABQ是等腰三角形,②当BQ=AB时,△ABQ是等腰三角形,③当BQ=AQ时,△ABQ是等腰三角形,分别求出点Q的坐标.
试题解析:(1)∵直线y=3x+m交y轴于点B(0,3),
∴m=3,
∴直线y=3x+3,
∴A(-1,0),
把A(-1,0),B(0,3),C(3,0)代入y=ax2+bx+c,得
 ,
,
解得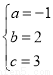 .
.
∴抛物线的解析式y=-x2+2x+3.
(2)如图1,连接BC,交对称轴一点,此点就是点P,使PA+PB最小,
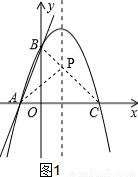
∵A,C关于对称轴对称,
∴此时PA+PB最小,
∵B(0,3),C(3,0)
∴直线BC的解析式为:y=-x+3,
∵对称轴为x=1,
∴P(1,2),
(3)存在
①如图2,当AQ=AB时,△ABQ是等腰三角形,
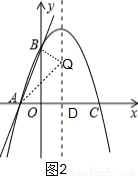
∵AB=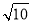
∴AQ=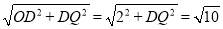
∴DQ=±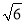
∴Q1(1,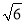 )Q2(1,-
)Q2(1,-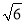 )
)
②如图3,当BQ=AB时,△ABQ是等腰三角形,
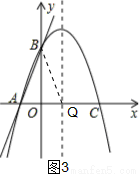
∵OA=1,OQ=1
∴Q3(1,0),
③如图4,当BQ=AQ时,△ABQ是等腰三角形,
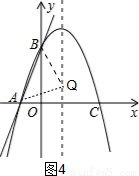
设Q(1,t),
∵A(-1,0),B(0,3),
∴(1+1)2+t2=12+(t-3)2,解得t=1,
∴Q4(1,1)
综上的所述:Q1(1,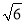 )Q2(1,-
)Q2(1,-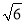 ),Q3(1,0),Q4(1,1).
),Q3(1,0),Q4(1,1).
考点:二次函数综合题.


科目:初中数学 来源:2014-2015学年云南省九年级上学期期中考试数学试卷(解析版) 题型:填空题
现有一个圆心角为90゜,半径为8cm的扇形纸片,用它恰好围成一个圆锥的侧面(接缝忽略不计),则该圆锥底面圆的半径= .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年云南省九年级上学期期中考试数学试卷(解析版) 题型:解答题
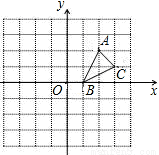
如图,方格纸中的每个小方格都是边长为1个单位的正方形,建立如图所示的平面直角坐标系,△ABC的顶点均在格点上,点B的坐标为(1,0)
①画出将△ABC绕原点O按顺时针旋转90°所得的△A1B1C1,并写出C1点的坐标是 ;
②求出点C在此过程中经过的路径长度(结果保留π).
查看答案和解析>>
科目:初中数学 来源:2014-2015学年云南省八年级上学期期中数学试卷(解析版) 题型:选择题
如果x2+mx+4是一个完全平方公式,那么m的值是( )
A.4 B.-4 C.±4 D.±8
查看答案和解析>>
科目:初中数学 来源:2014-2015学年云南省腾冲县九年级上学期五校联考摸底考试数学试卷(解析版) 题型:选择题
一元二次方程 与
与 的所有实数根之和为( )
的所有实数根之和为( )
A.2 B.-4 C.4 D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com