
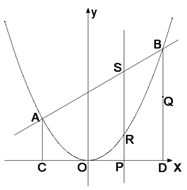
【题目】如图,二次函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象相交于
的图象相交于![]() 、
、![]() 两点,从点
两点,从点![]() 和点
和点![]() 分别引平行于
分别引平行于![]() 轴的直线与
轴的直线与![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点,点
两点,点![]() 为线段
为线段![]() 上的动点,过点
上的动点,过点![]() 且平行于
且平行于![]() 轴的直线与抛物线和直线分别交于
轴的直线与抛物线和直线分别交于![]() ,
,![]() .
.
(1)求一次函数和二次函数的解析式,并求出点![]() 的坐标.
的坐标.
(2)当SR=2RP时,计算线段SR的长.
(3)若线段BD上有一动点Q且其纵坐标为t+3,问是否存在t的值,使![]() .若存在,求
.若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】(1)y=x+4,y=![]() x2,B(4,8);(2)
x2,B(4,8);(2)![]() 或4;(3)-1.
或4;(3)-1.
【解析】(1)将A点坐标分别代入抛物线和直线的解析式中即可求出两函数的解析式.然后联立两函数的函数式形成方程组,即可求出B点的坐标.
(2)线段SR实际是直线AB的函数值和抛物线函数值的差.而RP的长实际是R点的纵坐标,根据SR=2RP可得出一个关于P点横坐标t的方程,据此可求出P点的横坐标t.然后代入SR的表达式即可求出SR的长.
(3)可用t表示出BQ的长,再根据D,P的坐标用t表示出R到BD的距离,然后根据三角形的面积公式即可得出△BRQ的面积表达式,根据其面积为15可求出t的值.
解:(1)由题意知点A(-2,2)在y=ax2的图象上,
又在y=x+b的图象上,
所以得2=a(-2)2和2=-2+b,
∴a=![]() ,b=4,
,b=4,
∴一次函数的解析式为y=x+4,
二次函数的解析式为y=![]() x2,
x2,
由 ,解得
,解得![]() ,
,
所以B点的坐标为(4,8);
(2)因过点P(t,0)且平行于y轴的直线为x=t,
所以点S的坐标(t,t+4),点R的坐标(t,![]() t2),
t2),
所以SR=t+4-![]() t2,RP=
t2,RP=![]() t2,
t2,
由SR=2RP得t+4-![]() t2=2×
t2=2×![]() t2,
t2,
解得t=-![]() 或t=2,
或t=2,
因点P(t,0)为线段CD上的动点,所以-2≤t≤4,
所以t=-![]() 或t=2,
或t=2,
当t=-![]() 时,
时,![]()
当t=2时,SR=2+4-![]() ×22=4,
×22=4,
所以线段SR的长为![]() 或4;
或4;
(3)因BQ=8-(t+3)=5-t,
点R到直线BD的距离为4-t,
所以S△BPQ=![]() ,
,
解得t=-1或t=10,
因为-2≤t≤4,所以t=-1.


科目:初中数学 来源: 题型:
【题目】如图,已知OP平分∠AOB,∠AOB=60°,CP=2,CP∥OA,PD⊥OA于点D,PE⊥OB于点E.如果点M是OP的中点,则DM的长是( ) 
A.2
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD⊥BC,AE平分∠BAC.
(1)若∠B=72°,∠C=30°,①求∠BAE的度数;②求∠DAE的度数;
(2)探究:如果只知道∠B=∠C+42°,也能求出∠DAE的度数吗?若能,请你写出求解过程;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)先化简,再求值:5(3a2b﹣ab2)﹣4(﹣ab2+3a2b),其中|a+1|+(b﹣![]() )2=0.
)2=0.
(2)先化简,再求值:﹣(3x2﹣4xy)﹣![]() [x2﹣2(4x﹣4xy)],其中x=﹣2.
[x2﹣2(4x﹣4xy)],其中x=﹣2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程(k﹣1)x2﹣2x+3=0有两个不相等的实根,则k的取值范围是( )
A.k< ![]()
B.k< ![]() 且k≠1
且k≠1
C.0≤k≤ ![]()
D.k≠1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某果园2011年水果产量为100吨,2013年水果产量为144吨,求该果园水果产量的年平均增长率.设该果园水果产量的年平均增长率为x,则根据题意可列方程为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面的表格是李刚同学一学期数学成绩的记录,根据表格提供的信息回答下面的问题
考试类别 | 平时 | 期中考试 | 期末考试 | |||
第一单元 | 第二单元 | 第三单元 | 第四单元 | |||
成绩 | 88 | 86 | 90 | 92 | 90 | 96 |

(1)李刚同学6次成绩众数是 .
(2)李刚同学6次成绩的中位数是 .
(3)李刚同学平时成绩的平均数是 .
(4)如果用下图的权重给李刚打分,他应该得多少分?(满分100分,写出解题过程)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com