
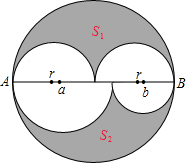
 如图,大圆的半径为r,直径AB上方两个半圆的直径均为r,下方两个半圆的直径分别为a,b.
如图,大圆的半径为r,直径AB上方两个半圆的直径均为r,下方两个半圆的直径分别为a,b.分析 (1)用半径为r的半圆的面积减去直径为r的圆的面积即可;
(2)用直径为(a+b)的半圆的面积减去直径为a的半圆的面积,再减去直径为b的半圆的面积即可;
(3)(4)将a=r+c,b=r-c,代入S2,然后与S1比较即可.
解答 解:(1)S1=$\frac{1}{2}π{r}^{2}$-$\frac{1}{4}π{r}^{2}$=$\frac{1}{4}π{r}^{2}$;
(2)S2=$\frac{1}{2}$π($\frac{a+b}{2}$)2-$\frac{1}{2}$$•\frac{1}{4}$πa2-$\frac{1}{2}•$$\frac{1}{4}$πb2,
=$\frac{1}{8}$π(a+b)2-$\frac{1}{8}$πa2-$\frac{1}{8}π{b}^{2}$
=$\frac{1}{4}πab$,
故答案为:$\frac{1}{4}πab$;
(3)选:C;
(4)将a=r+c,b=r-c,代入S2,得:
S2=$\frac{1}{4}π$(r+c)(r-c)=$\frac{1}{4}π$(r2-c2),
∵c>0,
∴r2>r2-c2,
即S1>S2.
故选C.
点评 此题考查了列代数式表示图形的面积,解题的关键是:结合图形分清各个半圆的半径及熟记圆的面积公式.


科目:初中数学 来源: 题型:填空题
 如图,四边形ABCD是菱形,O是两条对角线的交点,过O点的三条直线将菱形分成阴影和空白部分,当菱形的两条对角线的长分别为12和8时,则阴影部分的面积为24.
如图,四边形ABCD是菱形,O是两条对角线的交点,过O点的三条直线将菱形分成阴影和空白部分,当菱形的两条对角线的长分别为12和8时,则阴影部分的面积为24.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x(万元) | 1 | 2 |
| yA(万元) | 0.6 | 1.2 |
| yB(万元) | 2.4 | 4.4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
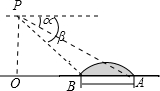 如图,直升飞机在跨河大桥AB的上方P点处,此时飞机离地面的高度PO=450m,且A、B、O三点在一条直线上,测得大桥两端的俯角分别为∠α=28°,∠β=43°,求大桥AB的长.(精确到1m)
如图,直升飞机在跨河大桥AB的上方P点处,此时飞机离地面的高度PO=450m,且A、B、O三点在一条直线上,测得大桥两端的俯角分别为∠α=28°,∠β=43°,求大桥AB的长.(精确到1m)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com