
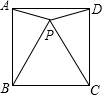
 如图,正方形ABCD中有一点P,边长为4,且△PBC是等边三角形,则∠APD=150°,S△APB=4.
如图,正方形ABCD中有一点P,边长为4,且△PBC是等边三角形,则∠APD=150°,S△APB=4. 分析 等边三角形内角为60°,且△ABP为等腰三角形,故可以求∠BAP,再求∠DAP,同理求∠ADP.根据三角形内角和为180°就可求∠APD.S△APB求出AB边上的高PM即可.
解答 解:作PM⊥AB于M.
∵△BCP为等边三角形,
∴∠PBC=60°,AB=BP=BC=CD,
∴∠ABP=30°∴∠BAP=75°,
∴∠DAP=15°,同理∠ADP=15°,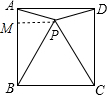
∴∠APD=150°.
在Rt△PMB中,PM=$\frac{1}{2}$PB=2,
S△APD=$\frac{1}{2}$×4×2=4
故答案为 150°,4.
点评 本题考查了正方形的性质,等边三角形的性质、等腰三角形的判定和性质,三角形的面积等知识,本题证明△ABP,△CDP是等腰三角形是解题的关键.


科目:初中数学 来源: 题型:填空题
 在平面直角坐标系中,直线l:y=x-1与x轴交于点A1,如图所示依次作正方形A1B1C1O、正方形A2B2C2C1、…、正方形AnBnCnCn-1,使得点A1、A2、A3、…在直线l上,点C1、C2、C3、…在y轴正半轴上,则点B2017的坐标是(22016,22017-1).
在平面直角坐标系中,直线l:y=x-1与x轴交于点A1,如图所示依次作正方形A1B1C1O、正方形A2B2C2C1、…、正方形AnBnCnCn-1,使得点A1、A2、A3、…在直线l上,点C1、C2、C3、…在y轴正半轴上,则点B2017的坐标是(22016,22017-1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠ACB=90°,D、E、F分别是AC、AB、BC的中点.
如图,在△ABC中,∠ACB=90°,D、E、F分别是AC、AB、BC的中点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
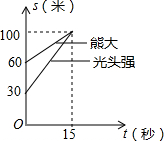 在动画片《熊出没》中,有一次光头强追赶熊大,在距离光头强家100米的地方追上了熊大,下图反映了这一过程,其中s表示光头强家的距离,t表示光头强追赶的时间,根据相关信息,以下说法错误的是( )
在动画片《熊出没》中,有一次光头强追赶熊大,在距离光头强家100米的地方追上了熊大,下图反映了这一过程,其中s表示光头强家的距离,t表示光头强追赶的时间,根据相关信息,以下说法错误的是( )| A. | 开始熊大与光头强之间的距离是30米 | |
| B. | 光头强跑了60米追上熊大 | |
| C. | 15秒后光头强追上了熊大 | |
| D. | 光头强追上熊大时,熊大跑了40米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
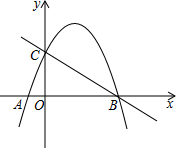 如图,在平面直角坐标系中,抛物线y=-$\frac{3}{4}$x2+bx+c与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,直线y=-$\frac{3}{4}$x+3经过B,C两点.
如图,在平面直角坐标系中,抛物线y=-$\frac{3}{4}$x2+bx+c与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,直线y=-$\frac{3}{4}$x+3经过B,C两点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com