练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
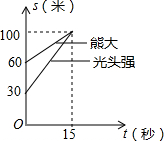
    13．在动画片《熊出没》中，有一次光头强追赶熊大，在距离光头强家100米的地方追上了熊大，下图反映了这一过程，其中s表示光头强家的距离，t表示光头强追赶的时间，根据相关信息，以下说法错误的是（　　）
    A．开始熊大与光头强之间的距离是30米
    B．光头强跑了60米追上熊大
    C．15秒后光头强追上了熊大
    D．光头强追上熊大时，熊大跑了40米

    分析 根据观察横坐标、纵坐标，可得答案．

    解答 解：A、开始熊大与光头强之间的距离是30米，正确；
    B、光头强跑了70米追上熊大，错误；
    C、15秒后光头强追上了熊大，正确；
    D、光头强追上熊大时，熊大跑了40米，正确；
    故选B

    点评 本题考查了函数图象，观察横坐标、纵坐标是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    3．声音在空气中传播的速度与气温的关系如下表，根据表格分析下列说法错误的是（　　）
    气温T/℃-20-10　0102030
    声速v/m/s318324330336342348
    A．在这个变化过程中，气温是自变量，声速是因变量
    B．声速随气温的升高而增大
    C．声速v与气温T的关系式为v=T+330
    D．气温每升高10℃，声速增加6m/s

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

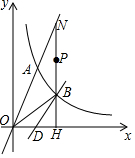    4．直线y=x-1交x轴于D点，交双曲线y=$\frac{k}{x}$（k＞0）于B点，直线y=2x交双曲线y=$\frac{k}{x}$（k＞0）于A点．
    （1）若A点横坐标为1，求B点坐标；
    （2）若OA=OB，求k；
    （3）在（2）中，过B点作BH⊥x轴于H，交OA于N点，P（2，t），比较PB与PN的大小．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    1．如图，正方形ABCD中有一点P，边长为4，且△PBC是等边三角形，则∠APD=150°，S△APB=4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

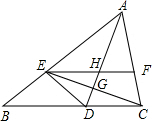    8．如图，AD是∠BAC平分线，点E在AB上，且AE=AC，EF∥BC交AC于点F，AD与CE交于点G，与EF交于点H．
    （1）证明：AD垂直平分CE；
    （2）若∠BCE=40°，求∠EHD的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．如图，在正方形ABCD中，点E是AD边上的一点，AF⊥BE于F，CG⊥BE于G．
    （1）若∠FAE=20°，求∠DCG的度数；
    （2）猜想：AF，FG，CG三者之间的数量关系，并证明你的猜想．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．阅读材料并解决问题：$\frac{1}{\sqrt{2}+1}$=$\frac{\sqrt{2}-1}{（\sqrt{2}+1）（\sqrt{2}-1）}$=$\frac{\sqrt{2}-1}{（{\sqrt{2}）}^{2}-{1}^{2}}$=$\sqrt{2}$-1，像上述解题过程中，$\sqrt{2}$+1与$\sqrt{2}$-1相乘的积不含二次根式，我们可以将这两个式子称为互为有理化因式，上述解题过程也称为分母有理化．
    （1）将下列式子进行分母有理化：①$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$；②$\frac{1}{\sqrt{3}-\sqrt{2}}$=$\sqrt{3}$+$\sqrt{2}$；
    （2）化简：$\frac{1}{\sqrt{3}+1}$+$\frac{1}{\sqrt{5}+\sqrt{3}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．关于x的一元二次方程x2-kx-6=0的根的情况为（　　）
    A．有两个不相等的实数根B．有两个相等的实数根
    C．无实数根D．无法确定根的情况

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．阅读材料：
    将等式$\sqrt{{5}^{2}}$=5反过来，可得到5=$\sqrt{{5}^{2}}$．根据这个思路，我们可以把根号外的因式“移入”根号内，用于根式的化简．例如：5$\sqrt{\frac{2}{5}}$=$\sqrt{{5}^{2}×\frac{2}{5}}$=$\sqrt{10}$．
    请你仿照上面的方法，化简下列各式：
    （1）3$\sqrt{\frac{1}{3}}$              
    （2）7$\sqrt{\frac{5}{7}}$                
    （3）8$\sqrt{\frac{3}{32}}$．

    查看答案和解析>>

    同步练习册答案