关于x的一元二次方程x2-kx-6=0的根的情况为( )A．有两个不相等的实数根B．有两个相等的实数根C．无实数根D．无法确定根的情况题目和参考答案——青夏教育精英家教网—

2．关于x的一元二次方程x²-kx-6=0的根的情况为（　　）

	A．	有两个不相等的实数根		B．	有两个相等的实数根
	C．	无实数根		D．	无法确定根的情况

分析先计算△=（-k）²-4×1×（-6）=k²+24＞0，即可判断方程根的情况．

解答解：∵△=（-k）²-4×1×（-6）=k²+24＞0，
∴一元二次方程x²-kx-6=0有两个不相等的实数，
故选A．

点评本题考查了一元二次方程ax²+bx+c=0（a≠0）的根的判别式△=b²-4ac：当△＞0，方程有两个不相等的实数根；当△=0，方程有两个相等的实数根；当△＜0，方程没有实数根．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：填空题

12．计算：3²⁰¹⁶×${（-\frac{1}{3}）}^{2017}$=-$\frac{1}{3}$．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

13．

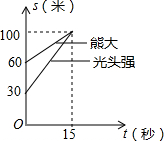在动画片《熊出没》中，有一次光头强追赶熊大，在距离光头强家100米的地方追上了熊大，下图反映了这一过程，其中s表示光头强家的距离，t表示光头强追赶的时间，根据相关信息，以下说法错误的是（　　）

	A．	开始熊大与光头强之间的距离是30米
	B．	光头强跑了60米追上熊大
	C．	15秒后光头强追上了熊大
	D．	光头强追上熊大时，熊大跑了40米

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

10．

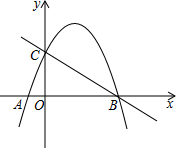如图，在平面直角坐标系中，抛物线y=-$\frac{3}{4}$x²+bx+c与x轴交于A，B两点（点A在点B的左边），与y轴交于点C，直线y=-$\frac{3}{4}$x+3经过B，C两点．
（1）求抛物线的解析式；
（2）点P为直线BC上方抛物线上的一个动点，且点P的横坐标为a，如果S_△PCB=2，求a的值；
（3）若点M为抛物线y=-$\frac{3}{4}$x²+bx+c上的一个动点，在直线BC上是否存在一点N，使得以M，N，C，O为顶点且以OC为边的四边形是平行四边形？若存在，请求出点N的坐标，若不存在，请说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

17．已知关于x的二次方程x²+mx+2m-n=0有两个相等的实数根2，求m，n的值．

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

7．

如图，点E为正方形ABCD边CB延长线上一点，点F为AB上一点，连接AE，CF，AC，若BE=BF，∠E=70°，则∠ACF=15°．