
 如图,字母A所代表的正方形面积为64.
如图,字母A所代表的正方形面积为64. 分析 根据正方形的面积等于边长的平方,由正方形PQED的面积和正方形PRQF的面积分别表示出PR的平方及PQ的平方,又三角形PQR为直角三角形,根据勾股定理求出QR的平方,即为所求正方形的面积.
解答 解:∵正方形PQED的面积等于225,
∴即PQ2=225,
∵正方形PRGF的面积为289,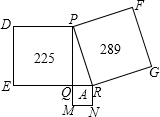
∴PR2=289,
又△PQR为直角三角形,根据勾股定理得:
PR2=PQ2+QR2,
∴QR2=PR2-PQ2=289-225=64,
则正方形QMNR的面积为64.
故答案为:64.
点评 此题考查了勾股定理以及正方形的面积公式.勾股定理最大的贡献就是沟通“数”与“形”的关系,它的验证和利用都体现了数形结合的思想,即把图形的性质问题转化为数量关系的问题来解决.能否由实际的问题,联想到用勾股定理的知识来求解是本题的关键.


科目:初中数学 来源: 题型:填空题
 如图,在 Rt△ABC中,∠ACB=90°,BC=6,AC=8,AB的垂直平分线 DE交 BC的延长线于F,则 CF的长为$\frac{7}{3}$.
如图,在 Rt△ABC中,∠ACB=90°,BC=6,AC=8,AB的垂直平分线 DE交 BC的延长线于F,则 CF的长为$\frac{7}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
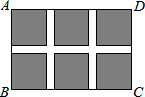 如图,某小区规划在一个长30m、宽20m的长方形ABCD土地上修建三条同样宽的通道,使其中两条与AB平行,另一条与AD平行,其余部分种花草.要使每一块花草的面积都为78m2,那么通道的宽应设计成多少m?设通道的宽为xm,由题意列得方程x2-35x+66=0.
如图,某小区规划在一个长30m、宽20m的长方形ABCD土地上修建三条同样宽的通道,使其中两条与AB平行,另一条与AD平行,其余部分种花草.要使每一块花草的面积都为78m2,那么通道的宽应设计成多少m?设通道的宽为xm,由题意列得方程x2-35x+66=0.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,等边△ABC的边长为2,P是BC边上的任一点(与B、C不重合),设BP=x,连接AP,以AP为边向两侧作等边△APD和等边△APE,分别与边AB、AC交于点M、N.
如图,等边△ABC的边长为2,P是BC边上的任一点(与B、C不重合),设BP=x,连接AP,以AP为边向两侧作等边△APD和等边△APE,分别与边AB、AC交于点M、N.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com