
【题目】如图所示,在直角梯形ABCD中,AD∥BC,∠A=90°,AB=12,BC=21,AD=16.动点P从点B出发,沿射线BC的方向以每秒2个单位长的速度运动,动点Q同时从点A出发,在线段AD上以每秒1个单位长的速度向点D运动,当其中一个动点到达端点时另一个动点也随之停止运动.设运动的时间为t(秒).
(1)设△DPQ的面积为S,求S与t之间的关系式;
(2)当t为何值时,四边形PCDQ是平行四边形?
(3)分别求出当t为何值时,①PD=PQ;②DQ=PQ.

【答案】(1)S=-6t+96;(2)当t=5时,四边形PCDQ是平行四边形;(3)①当t=![]() 时,PD=PQ;②当t=
时,PD=PQ;②当t=![]() 时,DQ=PQ
时,DQ=PQ
【解析】
(1)S=![]() DQAB,AQ=t,DQ=AD-AQ=16-t,将DQ和AB的长代入,可求出S与t之间的函数关系式;
DQAB,AQ=t,DQ=AD-AQ=16-t,将DQ和AB的长代入,可求出S与t之间的函数关系式;
(2)当四边形PCDQ为平行四边形时,PC=DQ,即16-t=21-2t,可将t求出;
(3)①当PD=PQ时,QE=ED=![]() QD,DE=162t,AE=BP=AQ+QE,即2t=t+162t,从而可将t求出;
QD,DE=162t,AE=BP=AQ+QE,即2t=t+162t,从而可将t求出;
②当DQ=PQ时,根据DQ2=PQ2即:t2+122=(16-t)2可将t求出.
(1)在直角梯形ABCD中,AD∥BC,∠A=90°,BC=21,AB=12,AD=16,
设AQ=t,BP=2t,则DQ=16t,PC=212t,
过点P作PE⊥AD于E,
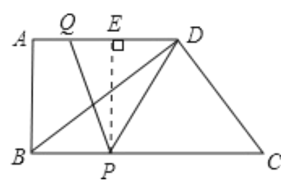
则四边形ABPE是矩形,PE=AB=12,
∴S=![]() DQAB=
DQAB=![]() (16t)×12=6t+96
(16t)×12=6t+96
故答案为:S=6t+96
(2)当四边形PCDQ是平行四边形时,PC=DQ,
∴212t=16t解得:t=5,
∴当t=5时,四边形PCDQ是平行四边形.
故答案为:当t=5时,四边形PCDQ是平行四边形
(3)∵AE=BP=2t,PE=AB=12,
①当PD=PQ时,QE=ED=![]() QD,
QD,
∵DE=162t,
∴AE=BP=AQ+QE,即2t=t+162t,
解得:t=![]() ,
,
∴当t=![]() 时,PD=PQ
时,PD=PQ
故答案为:当t=![]() 时,PD=PQ
时,PD=PQ
②当DQ=PQ时,DQ2=PQ2
∴t2+122=(16t)2解得:t=![]()
∴当t=![]() 时,DQ=PQ
时,DQ=PQ
故答案为:当t=![]() 时,DQ=PQ
时,DQ=PQ


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源: 题型:
【题目】某商场为做好“家电下乡”的惠民服务,决定从厂家购进甲、乙、丙三种不同型号的电视机108台,其中甲种电视机的台数是丙种的4倍,购进三种电视机的总金额不超过147 000元,已知甲、乙、丙三种型号的电视机的出厂价格分别为1 000元/台,1 500元/台,2 000元/台.
(1)求该商场至少购买丙种电视机多少台?
(2)若要求甲种电视机的台数不超过乙种电视机的台数,问有哪些购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售的一款空调机每台的标价是1635元,在一次促销活动中,按标价的八折销售,仍可盈利9%.
(1)求这款空调每台的进价(利润率=![]() =
=![]() ).
).
(2)在这次促销活动中,商场销售了这款空调机100台,问盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2﹣(2m+1)x+m(m+1)=0,
(1)求证:方程总有两个不相等的实数根;
(2)设方程的两根分别为x1、x2,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,A点坐标是(0,6),M点坐标是(8,0).P是射线AM上一点,PB⊥x轴,垂足为B.设AP=a.
(1)AM= ;
(2)如图,以AP为直径作圆,圆心为点C.若⊙C与x轴相切,求a的值;
(3)D是x轴上一点,连接AD、PD.若△OAD∽△BDP,试探究满足条件的点D的个数(直接写出点D的个数及相应a的取值范围,不必说明理由).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①为一种平板电脑保护套的支架效果图,AM固定于平板电脑背面,与可活动的MB、CB部分组成支架.平板电脑的下端N保持在保护套CB上.不考虑拐角处的弧度及平板电脑和保护套的厚度,绘制成图②.其中AN表示平板电脑,M为AN上的定点,AN=CB=20 cm,AM=8 cm,MB=MN.我们把∠ANB叫做倾斜角.
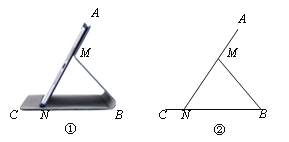
(1)当倾斜角为45°时,求CN的长;
(2)按设计要求,倾斜角能小于30°吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,平行四边形![]() 中,对角线
中,对角线![]() 的垂直平分线分别交
的垂直平分线分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,连接
,连接![]() 、
、![]() ;
;


(1)如图1,求证:四边形![]() 是菱形;
是菱形;
(2)如图2,当![]() ,点
,点![]() 在
在![]() 上,连接
上,连接![]() ,使
,使![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,作
,作![]() 于点
于点![]() ,连接
,连接![]() ,求证:
,求证:![]() ;
;
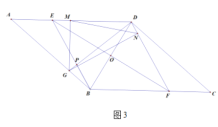
(3)如图3,在(2)的条件下,![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,
,![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系xOy中,A(0,4),B(8,0),C(8,4).
(1)试说明四边形AOBC是矩形.
(2)在x轴上取一点D,将△DCB绕点C顺时针旋转90°得到![]() (点
(点![]() 与点D对应).若OD=3,求点
与点D对应).若OD=3,求点![]() 的坐标.
的坐标.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com