
����Ŀ��ij�̳�Ϊ���á��ҵ����硱�Ļ���������ӳ��ҹ����ס��ҡ������ֲ�ͬ�ͺŵĵ��ӻ�108̨�����м��ֵ��ӻ���̨���DZ��ֵ�4�����������ֵ��ӻ����ܽ�����147 000Ԫ����֪�ס��ҡ��������ͺŵĵ��ӻ��ij����۸�ֱ�Ϊ1 000Ԫ/̨��1 500Ԫ/̨��2 000Ԫ/̨��
��1������̳����ٹ�����ֵ��ӻ�����̨��
��2����Ҫ����ֵ��ӻ���̨�����������ֵ��ӻ���̨����������Щ������
���𰸡���1�����ٹ�����ֵ��ӻ�10̨��
��2������һ�������ס��ҡ������ֲ�ͬ�ͺŵĵ��ӻ��ֱ�Ϊ40̨��58̨��10̨��
�������������ס��ҡ������ֲ�ͬ�ͺŵĵ��ӻ��ֱ�Ϊ44̨��53̨��11̨��
�������������ס��ҡ������ֲ�ͬ�ͺŵĵ��ӻ��ֱ�Ϊ48̨��48̨��12̨��
��������������8�֣���:��1���蹺����ֵ��ӻ�![]() ̨��������ֵ��ӻ�
̨��������ֵ��ӻ�![]() ̨���������ֵ��ӻ�
̨���������ֵ��ӻ�![]() ̨����������������������������������������������������������1��
̨����������������������������������������������������������1��
���������в���ʽ�� ![]() ����������2��
����������2��
���������ʽ��![]() ��������ٹ�����ֵ��ӻ�10̨������������������������������������3��
��������ٹ�����ֵ��ӻ�10̨������������������������������������3��
��2����������ã� ![]() �����
�����![]() ��������������������������������������������������������������4��
��������������������������������������������������������������4��
�֡�![]() ���������ɣ�1���ã�
���������ɣ�1���ã� ![]() ����
����![]() ��10��11��12����������ַ����� 5��
��10��11��12����������ַ����� 5��
����һ�������ס��ҡ������ֲ�ͬ�ͺŵĵ��ӻ��ֱ�Ϊ40̨��58̨��10̨����������6��
�������������ס��ҡ������ֲ�ͬ�ͺŵĵ��ӻ��ֱ�Ϊ44̨��53̨��11̨����������7��
�������������ס��ҡ������ֲ�ͬ�ͺŵĵ��ӻ��ֱ�Ϊ48̨��48̨��12̨����������8��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����AB�Ķ���B��Ϧ�������������һ��б���ϵĵ�D����ijУ��ѧ������ȤС���ͬѧ���ڲ�����˵ĸ߶ȣ�����˵ĵײ�A����õ�D������Ϊ15�㣬AC=10�ף��ֲ����BDA=45�㣮��֪б��CD���¶�Ϊi=1��![]() �������AB�ĸ߶ȣ�
�������AB�ĸ߶ȣ�![]() ��1.7�������ȷ����λ����
��1.7�������ȷ����λ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC����ֱ������ϵ�ڣ����С�CAB��90�㣬BC��5����A��B������ֱ�Ϊ(1��0)��(4��0)������ABC��x������ƽ�ƣ�����C����ֱ��y��2x��6��ʱ���߶�BCɨ�������Ϊ________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������ABCD��������AEFG��һ��������A����G��E�ֱ����߶�AD��AB�ϣ�����������AEFG�Ƶ�A��˳ʱ�뷽����ת������DG������ת�Ĺ����У����ܷ��ҵ�һ���߶εij����߶�DG�ij���ʼ����ȣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̵���Ҫ�����ס���������Ʒ��180��������ۺ��ۼ��������ע������=�ۼ۩����ۣ�
�� | �� | |
���ۣ�Ԫ/���� | 14 | 35 |
�ۼۣ�Ԫ/���� | 20 | 43 |
��1�����̵�ƻ�������������Ʒ���ܻ���1240Ԫ���ʼס���������ƷӦ�ֱ����ټ���
��2�����̵�ƻ�Ͷ���ʽ�����5040Ԫ����������������Ʒ���������1312Ԫ���������ļ��ֹ�����������ֱ��д�����л������Ĺ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A������Ϊ(4��0)����P��ֱ��y=![]()
![]() x+3�ڵ�һ�����ڵĵ㣬��P��PM
x+3�ڵ�һ�����ڵĵ㣬��P��PM![]() x���ڵ�M��O��ԭ�㣮
x���ڵ�M��O��ԭ�㣮
(1)���P������Ϊ(x, y)����������������y��ʾ��OPA�����S��
(2)S��y�������ĺ�����ϵ?�����Ա���y��ȡֵ��Χ��ʲô?
(3)�����P�������ʾ��OPA�����S��S��x�������ĺ�����ϵ?�����Ա�����ȡֵ��Χ��ʲô?
(4)��ֱ��y=![]()
![]() x+3����һ��Q��ʹ��QOA����OAΪ�ĵ��������Σ�
x+3����һ��Q��ʹ��QOA����OAΪ�ĵ��������Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У���C����B��AEƽ�֡�BAC��FΪ����AE��һ�㣨�����E�غϣ�����FD��BC��D��
��1�������F���A�غϣ��ҡ�C=50�㣬��B=30�㣬��ͼ1�����EFD�Ķ����� 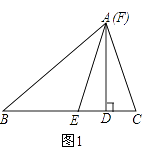
��2�������F���߶�AE�ϣ������A�غϣ�����ͼ2���ʡ�EFD���C����B��������������ϵ����˵�����ɣ� 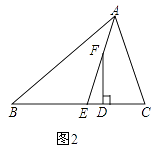
��3�������F�ڡ�ABC�ⲿ����ͼ3����ʱ��EFD���C����B��������ϵ�Ƿ�ᷢ���仯����˵�����ɣ� 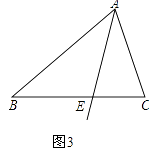
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У�AB=AC����D��BC���е㣬��E��AD��.
(1)��֤��BE=CE.
(2)��ͼ,��BE���ӳ��߽�AC�ڵ�F,��BF��AC,����ΪF,��BAC=45,ԭ����������������,��֤����AEF�ա�BCF.

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com