
【题目】在△ABC中,AB=AC,点D是BC的中点,点E在AD上.
(1)求证:BE=CE.
(2)如图,若BE的延长线交AC于点F,且BF⊥AC,垂足为F,∠BAC=45,原题设其它条件不变,求证:△AEF≌△BCF.

【答案】 (1)证明见解析 ;(2)证明见解析.
【解析】试题分析:(1)由等腰三角形的性质知∠BAE=∠CAE,由AB=AC、AE=AE利用“SAS”证△ABE≌△ACE即可;
(2)根据垂直定义求出∠AFB=∠BFC=∠ADB=90°,求出∠CBF=∠EAF,根据等腰三角形的判定推出AF=BF,根据ASA推出两三角形全等即可.
试题解析:证明:(1)∵AB=AC,D是BC的中点,∴∠BAE=∠CAE.
在△ABE和△ACE中,∵AB=AC ,∠BAE=∠CAE, AE=AE,∴△ABE≌△ACE(SAS),
∴BE=CE;
(2)∵AB=AC,点D是BC的中点,∴AD⊥BC,即∠ADC=90°,∴∠CAD+∠C=90°.
∵BF⊥AC,∠BAC=45°,∴∠CBF+∠C=90°,∠BFC=∠AFE=90°,BF=AF,∴∠CAD=∠CBF.
在△AEF和△BCF中,∵∠EAF=∠CBF, AF=BF ,∠AFE=∠BFC,∴△AEF≌△BCF(ASA).


科目:初中数学 来源: 题型:
【题目】某商场为做好“家电下乡”的惠民服务,决定从厂家购进甲、乙、丙三种不同型号的电视机108台,其中甲种电视机的台数是丙种的4倍,购进三种电视机的总金额不超过147 000元,已知甲、乙、丙三种型号的电视机的出厂价格分别为1 000元/台,1 500元/台,2 000元/台.
(1)求该商场至少购买丙种电视机多少台?
(2)若要求甲种电视机的台数不超过乙种电视机的台数,问有哪些购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,-2)
(1)求直线AB的表达式
(2)若直线AB上的点C在第一象限,且S△BOC=2,求点C的坐标

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列统计活动中不适宜用问卷调查的方式收集数据的是( )
A.某停车场中每天停放的蓝色汽车的数量
B.七年级同学家中电视机的数量
C.每天早晨同学们起床的时间
D.各种手机在使用时所产生的辐射
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,给出下列结论:
①abc>0;②b2=4ac; ③4a+2b+c>0;④3a+c>0,

其中,正确的结论是______.(写出正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD、BD相交于点F,点E在BD上,且![]() .
.
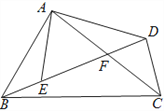
(1)试问:∠BAE与∠CAD相等吗?为什么?
(2)判断△ABE与△ACD是否相似?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列语句准确规范的是( )
A.直线a、b相交于一点m B.延长直线AB
C.反向延长射线AO(O是端点) D.延长线段AB到C,使BC=AB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,且抛物线经过A(-1,0),C(0,-5)两点,与x轴交于点B.
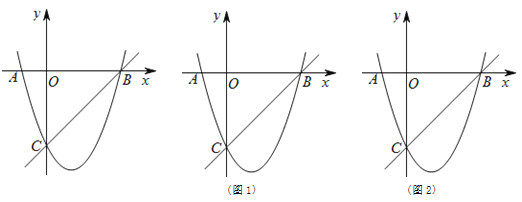
(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)设点P为抛物线上的一个动点,连接PB、PC,若△BPC是以BC为直角边的直角三角形,求此时点P的坐标;
(3)在抛物线上BC段有另一个动点Q,以点Q为圆心作⊙Q,使得⊙Q与直线BC相切,在运动的过程中是否存在一个最大⊙Q. 若存在,请直接写出最大⊙Q的半径;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场对今年端午节这天销售A、B、C三种品牌粽子的情况进行了统计,绘制如图1和2所示的统计图.根据图中信息解答下列问题: 
(1)这天共销售了多少个粽子?
(2)销售品牌粽子多个个?并补全图1中的条形图;
(3)求出A品牌粽子在图2中所对应的圆心角的度数;
(4)根据上述统计信息,明年端午节期间该商场对A、B、C三种品牌的粽子如何进货?请你提一条合理化的建议.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com