
【题目】如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,-2)
(1)求直线AB的表达式
(2)若直线AB上的点C在第一象限,且S△BOC=2,求点C的坐标

科目:初中数学 来源: 题型:
【题目】如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A,B的坐标分别为(1,0),(4,0),将△ABC沿x轴向右平移,当点C落在直线y=2x-6上时,线段BC扫过的面积为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A的坐标为(4,0).点P是直线y=![]()
![]() x+3在第一象限内的点,过P作PM
x+3在第一象限内的点,过P作PM![]() x轴于点M,O是原点.
x轴于点M,O是原点.
(1)设点P的坐标为(x, y),试用它的纵坐标y表示△OPA的面积S;
(2)S与y是怎样的函数关系?它的自变量y的取值范围是什么?
(3)如果用P的坐标表示△OPA的面积S,S与x是怎样的函数关系?它的自变量的取值范围是什么?
(4)在直线y=![]()
![]() x+3上求一点Q,使△QOA是以OA为底的等腰三角形.
x+3上求一点Q,使△QOA是以OA为底的等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠C>∠B,AE平分∠BAC,F为射线AE上一点(不与点E重合),且FD⊥BC于D;
(1)如果点F与点A重合,且∠C=50°,∠B=30°,如图1,求∠EFD的度数; 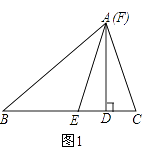
(2)如果点F在线段AE上(不与点A重合),如图2,问∠EFD与∠C﹣∠B有怎样的数量关系?并说明理由. 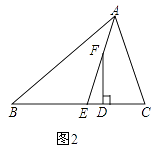
(3)如果点F在△ABC外部,如图3,此时∠EFD与∠C﹣∠B的数量关系是否会发生变化?请说明理由. 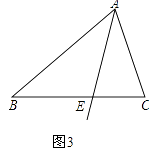
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义一种新运算“”,即mn=(m+2)×3﹣n,例如23=(2+2)×3﹣3=9.根据规定解答下列问题:
(1)求6(﹣3)的值;
(2)通过计算说明6(﹣3)与(﹣3)6的值相等吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D是BC的中点,点E在AD上.
(1)求证:BE=CE.
(2)如图,若BE的延长线交AC于点F,且BF⊥AC,垂足为F,∠BAC=45,原题设其它条件不变,求证:△AEF≌△BCF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请你根据萌萌所给的如图所的内容,完成下列各小题. 
(1)若m※n=1,m※2n=﹣2,分别求m和n的值;
(2)若m满足m※2≤0,且3m※(﹣8)>0,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com